Diffusion maps

擴散映射, Diffusion maps (以下簡稱 DM), 是個資料分析, 流型學習或是資料降維的工具.

這裡我們要介紹以 julia 來做 diffusion maps 降維.

Algorithm - diffusion maps embeding

先簡單介紹一下作法.

假設我們有 $n$ 筆 $d$ 維的資料, $$ \{x_1, x_2, \cdots, x_n\} \in R^d. $$

1. Affinity matrix $K$

我們需要先定一個 $K$ 矩陣, $K_{ij}=k(x_{i},x_{j})$, 一般而言我們使用 Guassian kernel $$ k(x,y) = e^{-\frac{\lVert x-y \rVert^2}{\sigma^2}}, $$ 其中 $\sigma$ 是個常數. 這樣造出來的 $K$ 矩陣會是個 $n\times n$ 對稱半正定的矩陣.

2. Normalized affinity matrix $Q$

接著我們要定 diffusion matrix $P$, 其定義為 $$ P=D^{-1}K, $$ 其中 $D$ 是個只有對角線有值的矩陣, 其元素為相對應 $K$ 矩陣的 rowsum, $D_{ii} = \sum^n_{j=1} K_{ij}$. 因此可以知道 $P$ 矩陣其實就是將 $K$ 矩陣的每個 row 做 normalize 的動作, 使其 rowsum 等於 $1$.

$P$ 這矩陣可看成是個機率矩陣, 其第 $i$ 個 row 表示從 $x_{i}$ 這個點跳到其他點的機率分佈.

接著我們考慮 $Q$ 矩陣, 定義為 $$ Q=D^{-\frac{1}{2}}KD^{-\frac{1}{2}}. $$ 我們可以很輕易發現 $P$ 以及 $Q$ 兩個矩陣有完全相同的 eigenvalues, 而 $P$ 的 eigenvectors 是 $$ v = D^{-1/2}v_Q, $$ 其中 $v_Q$ 是 $Q$ 的 eigenvector.

另一個重要觀察是 $Q$ 矩陣跟 $K$ 一樣是對稱半正定的矩陣, 因此它的 eigenvalues 都非負, 而且他的 eigenvalues 跟 singular values 會完全一模一樣.

3. 求出 $P$ 矩陣的 eigenvalues 跟 eigenvectors

先將 $Q$ 的 eigenvalues 跟 eigenvectors 都找出來, 接著 $P$ 的 eigenvalues 跟 eigenvectors 就依照上面的公式可以輕易得到.

我們令 $P$ 的 eigenvalues 跟 eigenvectors 分別為 $\lambda_i$ 跟 $\psi_i$, $1\le i\le n$.

需要注意的是, $\lambda_1=1$ 並且 $\psi_1$ 是一個常數向量, 因為我們要拿的是從第二個開始.

4. Define diffusion map $Y$

接著我們定義 $Y$ 矩陣為 $$ Y = \left[\lambda_2\psi_2, \lambda_3\psi_3, \cdots, \lambda_n\psi_n\right], $$ 這是個 $n\times (n-1)$ 的矩陣.

如果我們想要將原始資料投射到 $k$ 維, $k \le (n-1)$, 那我們就只要到第 $k+1$ 個 eigenvector 就好. 比如說要投影到三維, 我們只需要取 $$ Y = \left[\lambda_2\psi_2, \lambda_3\psi_3, \lambda_4\psi_4\right]. $$ 而 diffusion maps embedding 的每個點就是這個 $Y$ 矩陣的 row, 也就是 $y_i = Y(i,:)$.

Implementation in julia

接著我們就可以來看要怎樣以 julia 來做 diffusion maps.

我們需要以下幾個 packages:

using Plots
using Distances
using LinearAlgebra

以下例子為一個 spiral curve, 我們想要看經過 diffusion maps 的投射到二或三維後會長什麼樣子.

我們先把 spiral curve 上面的點造出來 (取 $300$ 個點)

# generating the data - a spiral curve
# n: number of sampling
n = 300;

theta = range(0,stop=6*pi,length=n);
r = range(0,stop=1, length=n);
# x and y-coordinates
x = r.*cos.(theta);
y = r.*sin.(theta);
# X is a n-by-2 data matrix
X = [x y];

畫出來看看原始 data 長怎樣. 我們照順序將點標為藍色, 紅色以及綠色.

plot(reshape(X[:,1], 100, 3), reshape(X[:,2], 100, 3), aspect_ratio=:equal, leg=false)

1. Affinity matrix $K$

先來造出 $K$ 矩陣:

E = pairwise(Euclidean(), X, dims=1);
sigma = 0.1;
K = exp.(-(E.^2)./(sigma^2));

2. Normalized affinity matrix $Q$

接著造出 $Q$ 矩陣, 並求出其 eigenvalues 跟 eigenvectors.

Q = zeros(n,n);
d_sq = zeros(n);
for ii = 1:n
    d_sq[ii] = sqrt(sum(K[ii,:]));
end
for ii = 1:n
    for jj = 1:n
        Q[ii,jj] = K[ii,jj]/(d_sq[ii]*d_sq[jj]);
    end
end
U,S,V = svd(Q);

3. 求出 $P$ 矩陣的 eigenvalues 跟 eigenvectors

$P$ 矩陣的 eigenvalues 跟 $Q$ 一樣, eigenvectors 也可以依公式得到:

for ii = 1 : n
    V[ii,:] = V[ii,:]/d_sq[ii];
end

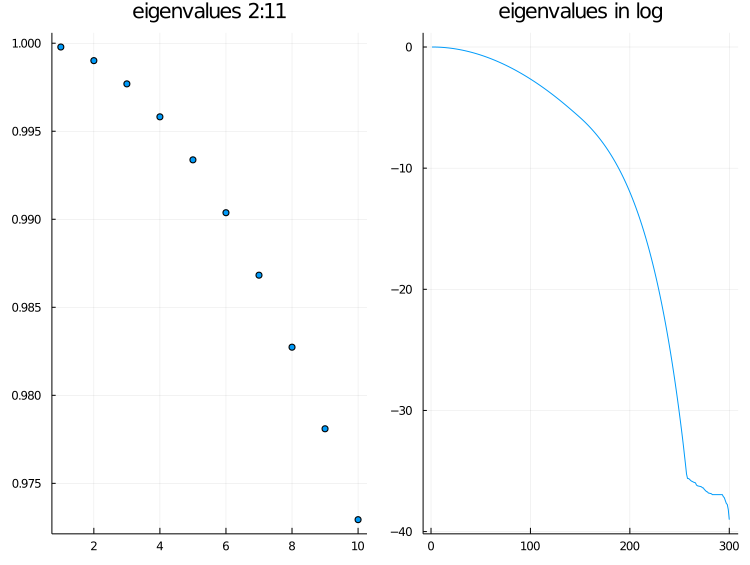
將 eigenvalues 畫出來看看. 左圖是第 $2$ 到第 $11$ 個, 右圖則是以 semilogy 畫出全部的 eigenvalues. 可以看出 eigenvalues 遞減的非常快, 所以其實 embedding 不需要取到全部 $(n-1)$ 維.

p1 = scatter(S[2:11], title="eigenvalues 2:11", leg=false);
p2 = plot(log.(S), title="eigenvalues in log", leg=false);
plot(p1, p2, layout=2, fmt=:png)

4. Define diffusion map $Y$

最後我們定義 embedding $Y$:

Y = zeros(n,3);
for ii = 1:3
    Y[:,ii] = V[:,ii+1].*S[ii+1];
end

我們知道 $Y$ 的每個 row 就是這個 embedding 的座標.

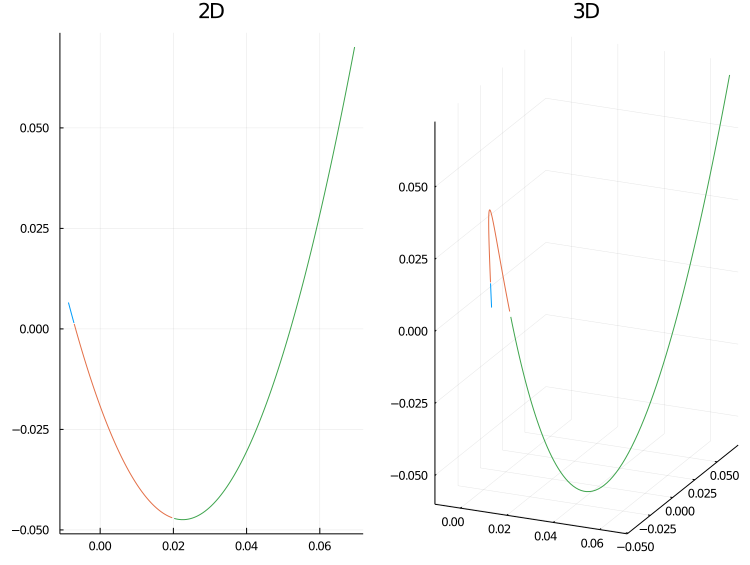
我們將 embedding 畫出來看看. 左圖是 embed 到二維, 右圖則是 embed 到三維.

p1 = plot(reshape(Y[:,1], 100, 3), reshape(Y[:,2], 100, 3), title="2D", leg=false)
p2 = plot(reshape(Y[:,1], 100, 3), reshape(Y[:,2], 100, 3), reshape(Y[:,3], 100, 3), title="3D", leg=false)
plot(p1, p2, layout=(1,2), fmt=:png)

我們一樣照順序將點標為藍色, 紅色以及綠色. 有趣的是, 我們發現這個 embedding 將整個 spiral curve 打開了. 因此, 經由 diffusion maps 投射之後我們比較榮以可以看出點資料真正在整個曲線上彼此間距離的遠近.

Extension

Diffusion maps 也常被拿來搭配 k-means 做成分群演算法, 算是 spectral clustering 的其中一種.

• Diffusion maps 的 python, julia 以及 matlab 程式都可以在這裡找到: Github - teshenglin/diffusion_maps.