主成分分析, Principal component analysis, 簡稱 PCA, 是個資料分析或是資料降維的工具.

資料降維簡單來說, 假設我們有一些資料, 這資料中的每一筆維度都很高, 導致我們很難 “看出” 或 “分析” 這資料集的特性, 這時候我們就會想要在低維度空間裡(通常三維以下)建構一組點資料, 並且想辦法使新的這組點資料在某些程度上能表示出原本高維度的點資料, 或保有某種特性. 這種將高維度資料在低維度表現出來的方式就稱為資料降維. 而 PCA 就是其中一種線性降維的方式.

這裡我們要談一下從數學角度來說 PCA 的原理及做法.

---

假設我們有 $n$ 筆 $p$ 維的資料, 記成 $$ \{x_1, x_2, \cdots, x_n\} \in R^p $$ 那我們想要做以下等價的兩件事:

1. 找到一組低維度的投影並且使得資料有 最大的變異性
2. 找到一組低維度的投影並且使得原始資料與投影後的資料之間的 距離平方和最小

Remark:

這裡所謂低維度的投影講精確一點, 事實上是在原本的 $R^p$ 空間中找到一個低維度的仿射子空間(affine subspace), 可以想像成一個不穿過原點的點或直線或平面, 找到之後再把原始資料點投影上去.

---

Example: 投影到 $0$ 維

先舉一個最簡單的例子, 假設我們想要投影到 $0$ 維, 也就是投影到一個點.

也就是說我們想要找一個點來代表整組資料.

直覺上來想, 如果我要幫一組資料找一個最具代表性的點, 應該就會用 “平均數” 或 “中位數” 來當這個點.

不過這邊我們需要講清楚的是究竟是以何種機制來做選擇的.

PCA 的做法就是要找一個點 $\mu\in R^p$ 使得所有資料點到這個點的距離平方和最小, 也就是要讓下式有最小值 $$ \sum_{i=1}^n \|x_i - \mu\|^2. $$ 簡單的微分求極值我們可以得到其最佳解為 $$ \mu = \frac{1}{n}\sum^n_{i=1} x_i, $$ 也就是原始資料點的平均值.

如果我們想要的是"距離"和最小而不是"距離平方"和, 也就是要使下式最小, $$ \sum_{i=1}^n \|x_i - \mu\|, $$ 則最佳解為資料的中位數. 證明可見 Median minimizes sum of absolute deviations.

---

Example: 投影到 $1$ 維

投影到 $0$ 維也許過於簡化, 接著我們來投影到 $1$ 維試試, 我們直接用圖形來說明:

藍色小圈就是原始資料點, 共10筆資料. 而 PCA 要做的事就是找到一個一維的 affine subspace, 就是中間那條斜線. 這樣我們就能把原始資料都投影到這個子空間去, 投影後的資料就是紅色點.

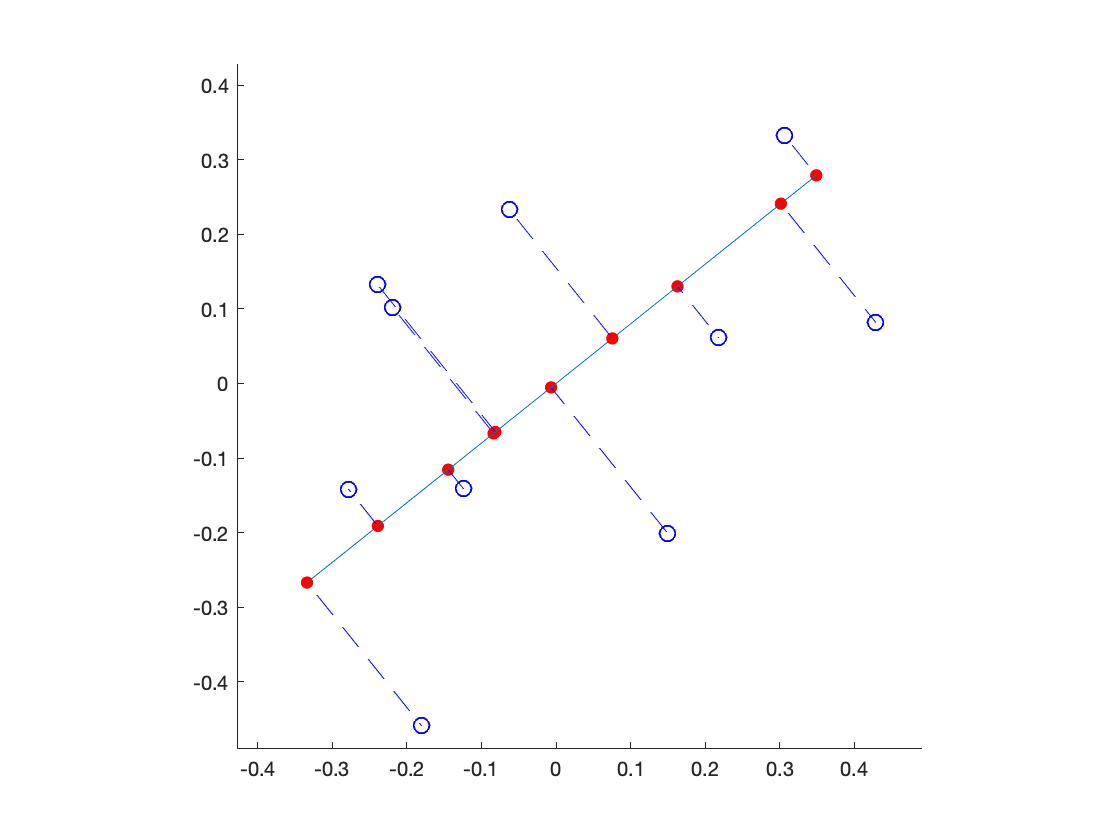
而這 affine subspace 怎麼找到的呢, 事實上這個子空間就是使得所有虛線段(原始資料到投影點連線)距離平方加起來最小的那個.

---

接下來我們來定義更一般的投影, 假設想要投影到 $k$ 維, $k\le p$, 也就是我們想要在 $R^p$ 空間中找一個 $k$ 維的 affine subspace, 使得說投影後資料與原始資料的距離平方和最小. 數學上來說就是要讓下式有最小值 $$ \sum_{i=1}^n \| x_i - (\mu + U\beta_i)\|^2, $$ 其中未知數有 $\mu\in R^p$, $U\in R^{p\times k}$, 以及 $\beta_i\in R^{k\times 1}$.

稍微解釋一下以上這些變數:

事實上這個 affine subspace 可以表示成 $$ \mu + V, \quad V = span\{u_1, \cdots, u_k\}, $$ 其中 $\mu$ 是 $R^p$ 空間中的一個點, $\{u_1, u_2, \cdots, u_k\}$ 是這 affine subspace 的基底, 收集在一起構成 $U$, 也就是 $U=[u_1, u_2, \cdots, u_k]$. 而 $\mu + U\beta_i$ 就是 $x_i$ 這個資料點在這 affine subspace 上的投影, 所以 $\beta_i$ 可以想像是原始資料第 $i$ 筆投影到 affine subspace 之後的座標, 或是係數.

此外, 我們可以特別要求這基底要正交, 也就是 $U^TU = I_k$, 其中 $I_k$ 表示 $k\times k$ 的 identity matrix.

---

再稍微整理一下, 我們想要找到 $\mu$, $U$ 以及 $\beta_i$ 使得下式 $E$ 有最小值 $$ E = \sum_{i=1}^n \|x_i - (\mu + U\beta_i)\|^2, $$ 其中有兩個條件, $U^TU=I_k$, 以及 $\sum^n_{i=1} \beta_i=\vec{0}$.

Remark:

第二個條件 $\sum_i \beta_i=\vec{0}$ 看起來似乎是憑空冒出來的, 不過這可以從兩方面來說.

1. 我們希望投影之後的解他們的平均是 $0$, 所以新資料點的中心就在新座標原點的位置.
2. 數學上來說, 其實 $\mu$ 並沒有唯一性. 也就是雖然 affine subspace 表示成 $\mu +V$, 但是這個 $\mu$ 是這子空間裡的任何一個點都可以. 為了讓解有唯一性我們加了這個條件.

---

這問題可以被完全解出來, 也就是說給定 $x_i$, 我們可以決定出最佳的 $\mu$, $U$ 以及 $\beta_i$ 使得上式的值為最小.

推導過程我們在這先省略, 有興趣的請見 references, 或是 主成分分析 - 2.

其最佳解整理如下:

1. $\mu$ 就剛好是投影到 $0$ 維的解, 也就是資料點的平均: $$ \mu = \frac{1}{n}\sum^n_{i=1} x_i $$

2. 找到平均後我們將所有資料做平移使得中心為原點, 定 $y_i = x_i-\mu$, 求出這組新資料的共變異數矩陣 $\Sigma=YY^T$, 其中 $Y=[y_1, \cdots, y_n]$ 是個 $p\times n$ 的矩陣, 而 $\Sigma$ 則是 $p\times p$.

   對 $\Sigma$ 做譜分解(spectral decomposition), 找到其最大的 $k$ 個 eigenvalues 以及相對應的 eigenvectors, 將 eigenvectors 收集起來就得到 $U=[u_1, \cdots, u_k]$, 也就是 affine subspace 的 basis.

3. 將原資料投影到此 affine subspace 中得到 $\beta_i$, 也就是 $$ \beta_i = \sum^k_{j=1}<u_j, (x_i-\mu)> $$

---

一般最基礎的 PCA 做法就是從 $x_i$, 得到 $\mu$. 將資料平移求出 $y_i$, 接著求共變異數矩陣 $\Sigma$. 接著對 $\Sigma$ 做 eigen-decomposition 求出其特徵值及特徵向量. 拿出最大的幾個就可以定出 affine subspace. 然後將 $y_i$ 投影下去就得到 $\beta_i$, 也就是投影之後的座標了.

以上這做法的 Matlab 程式如下:

$X$ 是 $p\times n$ 的 data matrix 含有 $p$ 個 features 以及 $n$ 個 samples.

投影到 $k$ 維子空間, 投影後得到 $B$, 為 $k\times n$ 的 data matrix.

% Matlab program
function B = principal_component_analysis(X, k)

%   Input: X, p*n data matrix, p 個 features 以及 n 個 samples
%          k, 要降到的維度, k 為正整數, k<=p
%   Output: B: k*n data matrix, k 個 features 以及 n 個 samples

    [p, n] = size(X);               % p 個 features 以及 n 個 samples
    mu = sum(X, 2)/n;               % 計算 sample 的平均 mu
    Y = X - mu*ones(1,n);           % 資料平移得到 Y
    S = Y*Y';                       % 求出共變異數矩陣 S
    [U, D] = eig(S, 'vector');      % 求出特徵值 D 及特徵向量 U
    [D, ind] = sort(D, 'descend');  % 將特徵值由大到小排列
    U = U(:, ind);                  % 將特徵向量照樣排列
    B = U(:,1:k)'*Y;                % 投影到前 k 個組成的空間中並求出係數 B
end

Remark:

這做法會造出一個 $p\times p$ 的共變異數矩陣 $\Sigma$, 並且算出全部的特徵值及特徵向量. 不過其實我們只需要前 $k$ 個. 所以多出來的部分會丟掉, 有點浪費.

---

我們再來看一下這個共變異數矩陣 $\Sigma=YY^T$, 可以很輕易地看出來這是個對稱矩陣, 所以特徵值一定是實數, 也一定存在 orthonormal 的實數特徵向量組. 因此我們以上的要求(將特徵值按大小排列, 特徵向量要彼此正交)都一定做得到. 而分解之後可以得到 $$ \Sigma = U\Lambda U^T, $$ 其中 $U$ 是個 $p\times p$ 矩陣.

事實上由 $\Sigma=YY^T$ 可以知道 $\Sigma$ 一定是個半正定矩陣, 所以它的 eigenvalues 一定都非負.

我們事實上可以將矩陣 $Y$ 做奇異值分解 (Singular Value Decomposition, SVD), 得到 $$ Y = \hat{U}\hat{\Sigma}\hat{V}^T, \quad \hat{U}\in R^{p\times p}, \quad \hat{\Sigma}\in R^{p\times n}, \quad \hat{V}\in R^{n\times n}, $$ 並且 $\hat{U}$ 及 $\hat{V}$ 都是 orthogonal matrix, 也就是 $\hat{U}^T\hat{U}=I_p$ 以及 $\hat{V}^T\hat{V}=I_n$.

既然我們有 $\Sigma=YY^T$, 很容易可以看出來其實 $$ U = \hat{U}, \quad \Lambda = \hat{\Sigma}\hat{\Sigma}^T\in R^{p\times p}. $$ 也就是說將 $Y$ 的 singular values 平方就可以得到 $\Sigma$ 的 eigenvalues. 而 $Y$ 的 left singular vectors 事實上就是 $\Sigma$ 的 eigenvectors.

而投影後的係數我們可以算一下: $$ B=U^TY = \hat{U}^T\hat{U}\hat{\Sigma}\hat{V}^T = \hat{\Sigma}\hat{V}^T. $$ 所以如果我們只需要投影後的係數, 將 $Y$ 做 SVD 並且我們需要的是 $Y$ 的 right singular vectors.

---

Remark:

以上這式子很有趣, 告訴我們投影之後的座標 $B$ 與投影之前的座標 $Y$ 的 SVD 之間的關係. 另一種降維方法: Multidimensional scaling (MDS) 在某些情況下會有一模一樣的關係. 這樣就把兩種方法 PCA 跟 MDS 連在一起了. 雖然出發點不一樣, 竟然(在某些情況下)結果是一樣的!

---

利用以上關係我們可以將程式改寫如下:

% Matlab program
function B = principal_component_analysis2(X, k)

%   Input: X, p*n data matrix, p 個 features 以及 n 個 samples
%          k, 要降到的維度, k 為正整數, k<=p
%   Output: B: k*n data matrix, k 個 features 以及 n 個 samples

    [p, n] = size(X);               % p 個 features 以及 n 個 samples
    mu = sum(X, 2)/n;               % 計算 sample 的平均, mu
    Y = X - mu*ones(1,n);           % 資料平移得到 Y
    [~, S, V] = svds(Y, k);         % 將 Y 做奇異值分解並取前 k 個 eigenvectors
    B = S*V';                       % 求出投影後的係數
end

---

而事實上, matlab 已經內建 PCA 程式了, 所以其實完全不用自己寫. 只是要注意一下 matlab 裡 PCA 的輸入 sample points 是 $n\times p$, 由於我們以上都是將 $X$ 設成 $p\times n$ 的矩陣, 所以要轉置一下, 程式只有兩行, 如下:

% Matlab program
[U, B] = pca(X');
B = B(:,1:k)';

---

Working example

這裡我們舉一個例子, 我們先構造 sample points, 是一個類似螺旋狀結構, 程式如下:

% Matlab program
n = 1000;                                   % 取 n 個點
t = 3*pi*(1:n)/n;                           % 利用參數化來構造, 取 t\in[0, 3*pi]
X = [t.*cos(t); 5*rand(1,n); t.*sin(t)];    % 先利用 random 構造三圍中的一個面
M = makehgtform('axisrotate',[1 1 1], 30);  % 構造旋轉矩陣
X = M(1:3, 1:3)*X + 10*rand(3,1)*ones(1,n); % 將 sample 旋轉並且隨機平移

其圖形長這樣:

scatter3(X(1,:), X(2,:), X(3,:), [], (1:n)/n, 'fill')

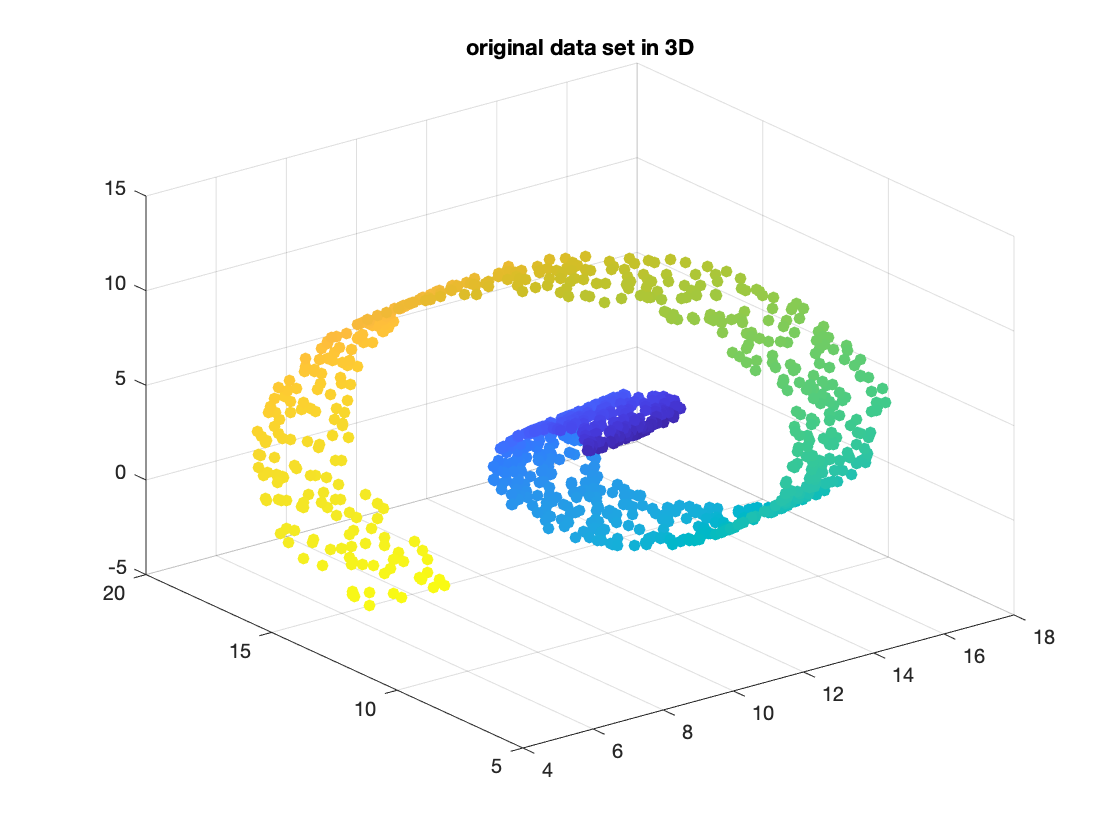
接著我們用 PCA 投影到二維, 圖形長這樣:

[~, B] = pca(X');
B=B';
scatter(B(1,:), B(2,:), [], (1:n)/n, 'fill')

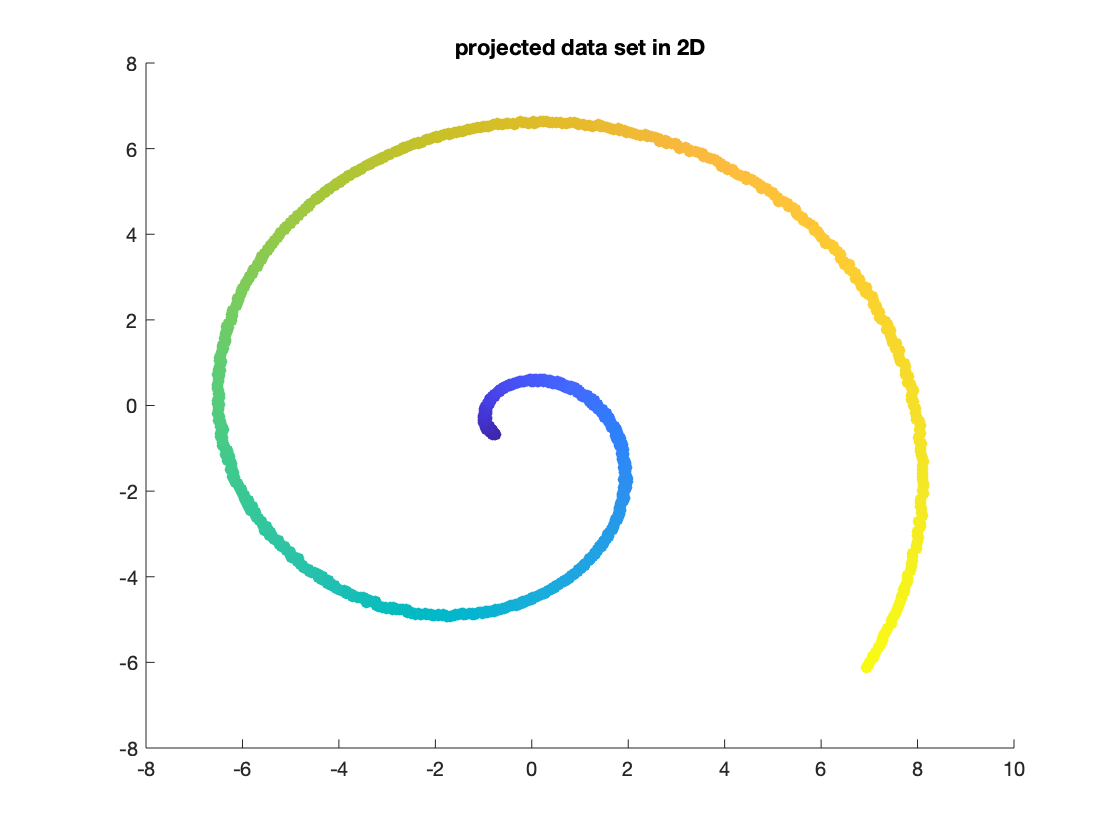
可以發現 PCA 找到一個正確的軸來做投影, 使得原本的螺旋線可以看得很清楚.

---

Extension

• 另一種降維方法: Multidimensional scaling (MDS).
• PCA 推導過程及證明: 主成分分析 - 2

---

References:

1. NCTS mini-course on manifold learning
2. What is principal component analysis?

---