Sec.5.2 - Area functions
Discovery Project in Sec.5.2, Calculus by Stewart
Chinese version 面積函數
Question 1(a):
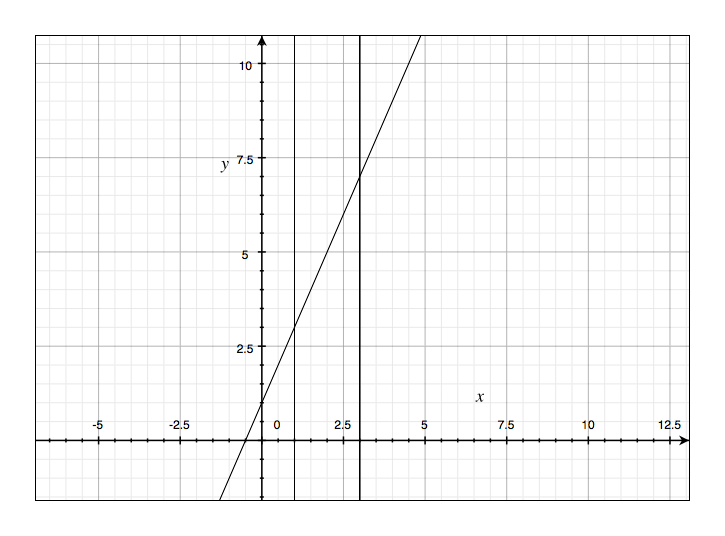
Draw the line $y = 2t+1$ and use geometry to find the area under this line, above the t-axis, and between the vertical lines $t=1$ and $t = 3$.
Answer:
let $f(x)=y=2t+1$, then $f(1)=3$ and $f(3)=7$.
So, Area$= \frac{1}{2}(3+7)(3-1) = 10$
Question 1(b):
If $x>1$, let $A(x)$ be the area of the region that lies under the line $y = 2t + 1$ between $t =1$ and $t = x$. Sketch this region and use geometry to find expression for $A(x)$.
Answer:
$f(1)=3$ and $f(x)=2x+1$.
Area$= A(x) = \frac{1}{2}(2x+1+3)(x-1) = x^2 +x -2 $
Question 1(c):
Differentiate the area function $A(x)$. What do you notice?
Answer:
Because $A(x) = x^2+x-2$, then $A’(x) = 2x+1$.
We can found that $A’(x)$ have the same form with $f(x) = y = 2t+1$.
Question 2(a):
If $x \geq -1$, let $$ A(x) = \int_{-1}^{x} (1+t^2)dt $$ $A(x)$ represents the area of a region. Sketch that region.
Answer:
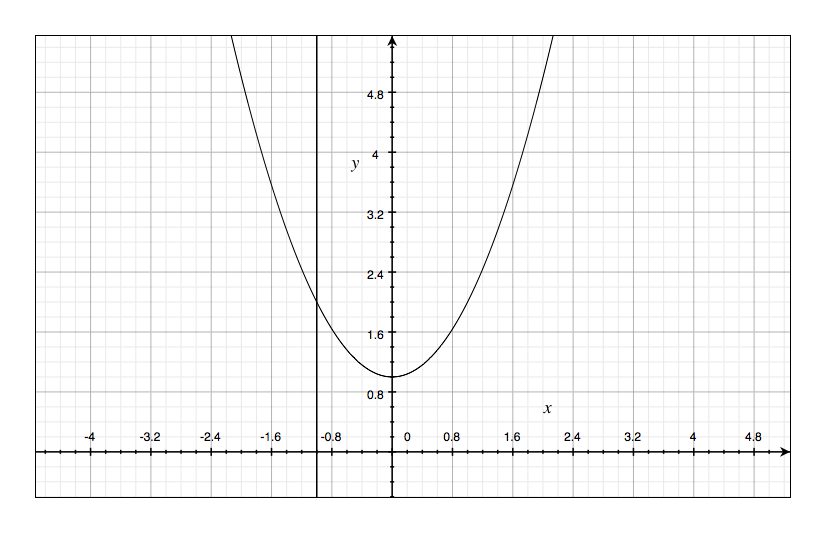
Question 2(b):
Use the result of Exercise 5.2.28 to find an expression for $A(x)$.
Answer:
$$ A(x) = \int_{-1}^{x} (1+t^2)dt =\frac{t^3-(-1)^3}{3}+x+1 $$
Question 2(c):
Find $A’(x)$. What do you notice?
Answer:
$A’(x) = 1+t^2$, we can found that $A’(x)$ is the upper bound of the area of a region.
Question 2(d):
If $x \geq -1$ and h is a small positive number, then $A(x+h) - A(x)$ represents the area of a region. Describe and sketch the region.
Answer:
The area is trapezoid, the length of base is $h$ ,and the length of parallel sides is $A(x+h)$ and $A(x)$ ,respectively.
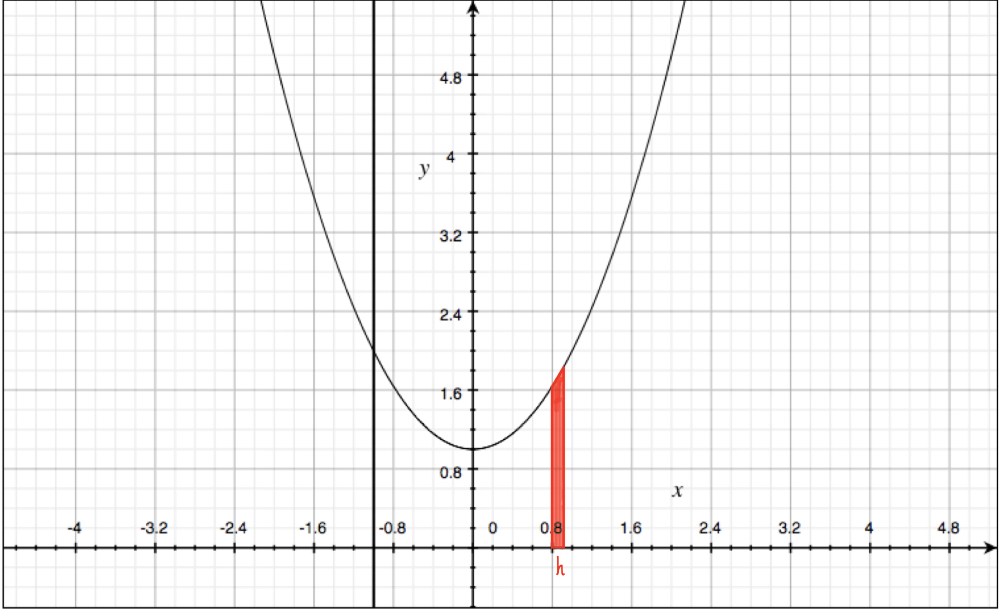
Question 2(e):
Draw a rectangle that approximates the region in part (d). By comparing the areas of these two regions, show that $$ \frac{A(x+h)-A(x)}{h} \approx 1+x^2 $$
Answer:
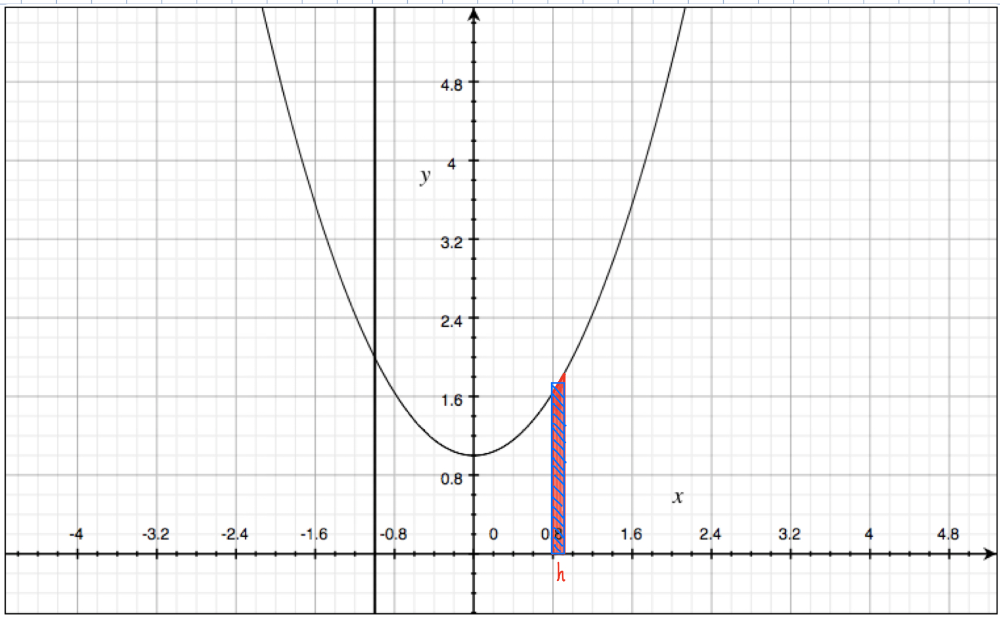
Question 2(f):
Use part (e) to give an intuitive explanation for the result of part (c).
Answer:
As you can see, the result of part (c) is equal to the result of part (e) ,which means when we cut the area into infinite areas, the result will equal to the differentiate of the formula.
Question 3(a):
Draw the graph of the function $f(x)=cos(x^2)$ in the viewing rectangle $[0,2]$ by $[-1.25,1.25]$
Answer:
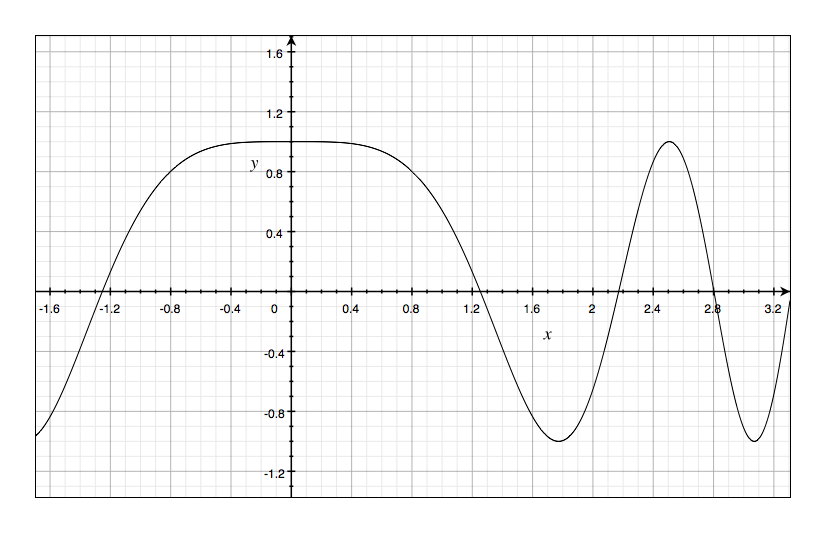
Question 3(b):
If we define a new function $g$ by $$ g(x) = \int_{0}^{x}\cos(t^2) dt $$ then $g(x)$ is the area under the graph of $f$ from $0$ to $x$ [until $f(x)$ becomes negative, at which point $g(x)$ becomes a difference of areas.] Use part (a) to determine the value of $x$ at which $g(x)$ starts to decrease. [Unlike the integral in Problem 2, it is impossible to evaluate the intergral defining $g$ to obtain an explicit expression for $g(x)$]
Answer:
According to part (a), we can found that $g(x)$ starts to decrease when the line goes under x-axis. Thus, $x^2 = \pi \to x\approx1.77245$
Question 3(c):
Use the integration command on your calculator or computer to estimate $g(0.2)$, $g(0.4),g(0.6),\cdots,g(1.8),g(2)$. Then use these values to sketch a graph of $g$.
Answer:
$g(x)$ is the blue line in the graph.
| x | g(x) |
|---|---|
| 0.2 | 0.2 |
| 0.4 | 0.399 |
| 0.6 | 0.5923 |
| 0.8 | 0.7678 |
| 1 | 0.9045 |
| 1.2 | 0.9739 |
| 1.4 | 0.9498 |
| 1.6 | 0.8255 |
| 1.8 | 0.6354 |
| 2 | 0.4615 |
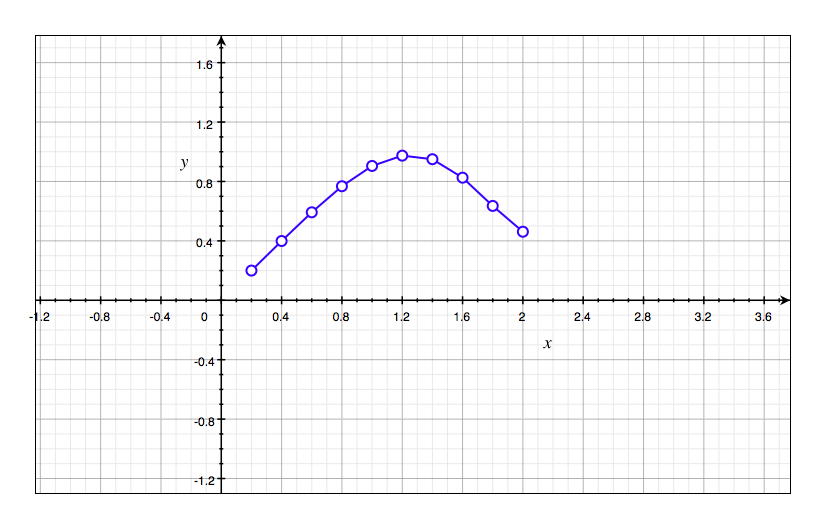
Question 3(d):
Use your graph of $g$ from part (c) to sketch the graph of $g’$ using the interpretation of $g’(x)$ as the slope of a tangent line. How does the graph of $g’$ compare with the graph of $f$ ?
Answer:
We can found that $g’(x)$ is almost the same with the graph of $f$.
| x | g’(x) |
|---|---|
| 0.3 | 0.995 |
| 0.5 | 0.9665 |
| 0.7 | 0.8775 |
| 0.9 | 0.6835 |
| 1.1 | 0.347 |
| 1.3 | -0.1205 |
| 1.5 | -0.6215 |
| 1.7 | -0.9505 |
| 1.9 | -0.8695 |
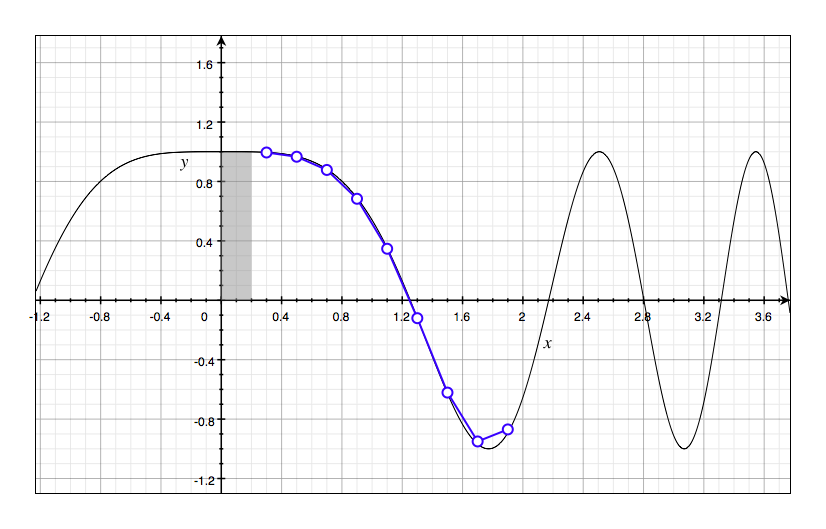
Question 4:
Suppose $f$ is a continuous function on the interval $[a,b]$ and we define a new function $g$ by the equation $$ g(x) = \int_{a}^{x} f(x)dt $$ Based on your result in Problem 1-3, conjecture an expression for $g’(x)$.
Answer:
Based on the result in Problem 1-3, we can conjecture that $g’(x) = f(x)$.