Sec.11.11 - Radiation From The Stars
Applied Project in Sec.11.11, Calculus by Stewart
Chinese version 恆星的輻射
Any object emits radiation when heated. A blackbody is a system that absorbs all the radiation that falls on it. For instance, a matte black surface or a large cavity with a small hole in its wall (like a blastfurnace) is a blackbody and emits blackbody radiation. Even the radiation from the sun is close to being a blackbody radiation.
Proposed in the late 19th century, the Rayleigh-Jeans Law expresses the energy density of blackbody radiation of wavelength $\lambda$ as $$ f(\lambda)=\frac{8 \pi kT}{\lambda^4} $$ where $\lambda$ is measured in meters, $T$ is the temperature in kelvins (K) and $k=$ Boltzmann’s constant $=1.3807\times 10^{-23}$J/K.
The Rayleigh-Jeans Law agrees with experimental measurements for long wavelengths but disagrees drastically for short wavelengths. [The law predicts that $f(\lambda)\rightarrow \infty$as $\lambda \to 0^+$ but experiments have shown that $f(\lambda)\to0$.] This fact is known as the ultraviolet catastrophe.
In 1990 Max Planck found a better model (known now as Planck’s Law) for blackbody radiation: $$ f(\lambda)= \frac{8 \pi hc \lambda^{-5}}{e^{hc/(\lambda kT)}-1} $$ and
- $h=$ Planck’s constant $=6.6262\times 10^{-34}$ J$\cdot$s
- $c=$ speed of light $=2.997925\times10^8$m/s
Question 1:
Use l’Hospital’s Rule to show that
$$ \lim_{\lambda\to0^+}f(\lambda)=0 $$ and $$ \lim_{\lambda\to\infty} f(\lambda) = 0 $$
for Planck’s Law. So this law models blackbody radiation better than the Rayleigh-Jeans Law for short wavelengths.
Question 2:
Use a Taylor polynomial to show that, for large wavelengths, Planck’s Law gives approximately the same values as the Rayleigh-Jeans Law.
Question 3:
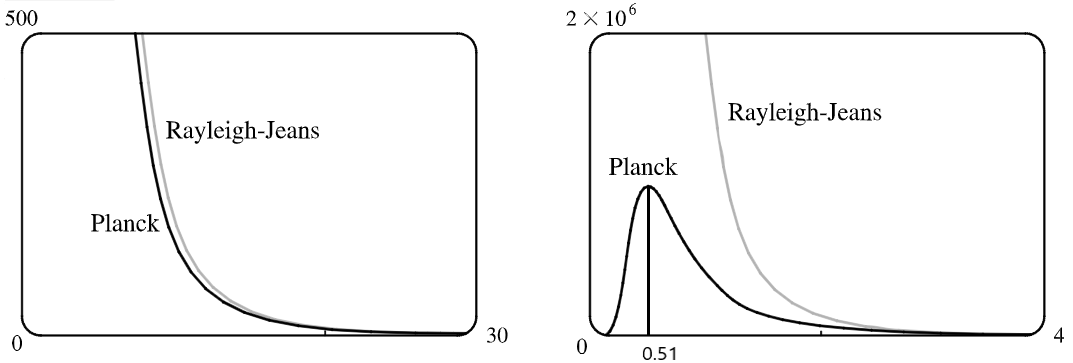
Graph $f$ as given by both laws on the same screen and comment on the similarities and differences. Use $T=5700$K (the temperature of the Sun ). (You may want to change from meters to the more convenient unit of micrometers: $1\mu$m $=10^{-6}$m.)
Answer:
To convert to $\mu$m, we substitute $\lambda/10^6$ for $\lambda$ in both laws. For large $\lambda$ (left), the graphs of two laws are similar. For small $\lambda$ (right), the graphs of two laws are very different.
Question 4:
Use your graph in Problem 3 to estimate the value of $\lambda$ for which $f(\lambda)$ is a maximum under Planck’s Law.
Answer:
From the graph in Problem 3, $f(\lambda)$ has a maximum under Planck’s Law at $\lambda\approx0.51 \mu$m.
Question 5:
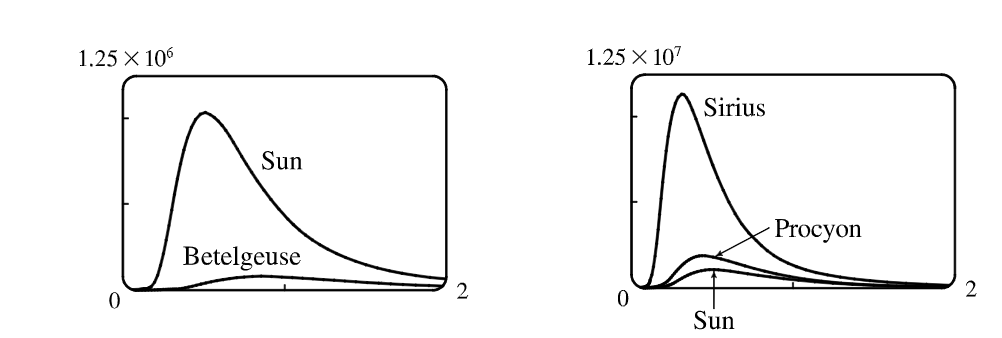
Investigate how the graph of $f$ changes as $T$ varies. (Use Planck’s Law.) In particular, graph $f$ for the stars
- Betelgeuse ($T=3400$K)
- Procyon ($T=6400$K)
- Sirius ($T=9200$K)
- Sun
How does the total radiation emitted (the area under the curve) vary with $T$ ? Use the graph to comment on why Sirius is known as a blue star and Betelgeuse as a red star.
Answer:
As $T$ gets larger, the total area under the curve increase, so we can consider that the hotter the star is, the more energy it emits. Also as $T$ increases, the maximum $\lambda$-value decreases, so the higher the temperature, the shorter the peak wavelength and the average wavelength of light emitted. This is why Sirius is a blue star and Betelgeuse is a red star. And most of its light is of a short wavelength. That is, a higher frequency, toward the blue end of the spectrum, whereas most of Betelgeuse’s light is of a lower frequency, toward the red end of the spectrum.