Sec.4.1 - 彩虹的微積分學
Applied Project in Sec.4.1, Calculus by Stewart
英文版請見 The Calculus of ranbows
當陽光照射到半空中的雨滴,光線被散射就會形成彩虹。彩虹自古以來就被人類著迷著,且早在亞里士多德時代以來激發許多人們進行科學的探討,並嘗試找到解釋。在這份專題裡,我們使用笛卡爾和牛頓的思想來解釋彩虹的形狀、位置和顏色。
問題 1:
下面這張圖顯示了一道光束從 A 點進入球形雨滴。有一些光被反射,但線段AB 表示了一些沒有被反射,而穿入雨滴的光線軌跡。這裡要注意的是,這道光線是朝法線AO 折射的,而實際上,斯涅爾定律提及 $\sin\alpha = k\sin\beta$ ,其中 $\alpha$ 是入射角,$\beta$ 是折射角,而 $k\approx\frac{4}{3}$ 是水的折射率。在 B 點,有一些光線穿過水滴,然後折射進入空氣,但依然有部分被反射,如線段BC所示。 (入射角等於反射角)當光束到達 C 點時,它的一部份會被反射,但讓我們更感興趣的是從 C 點離開雨滴部分(要注意它是從法線折射出去的)。偏差角 $D(\alpha)$ 是光束在此三階段過程中經歷的順時針旋轉量。因此, $$ D(\alpha ) = (\alpha - \beta ) + (\pi - 2\beta ) + (\alpha - \beta) = \pi + 2\alpha - 4\beta. $$
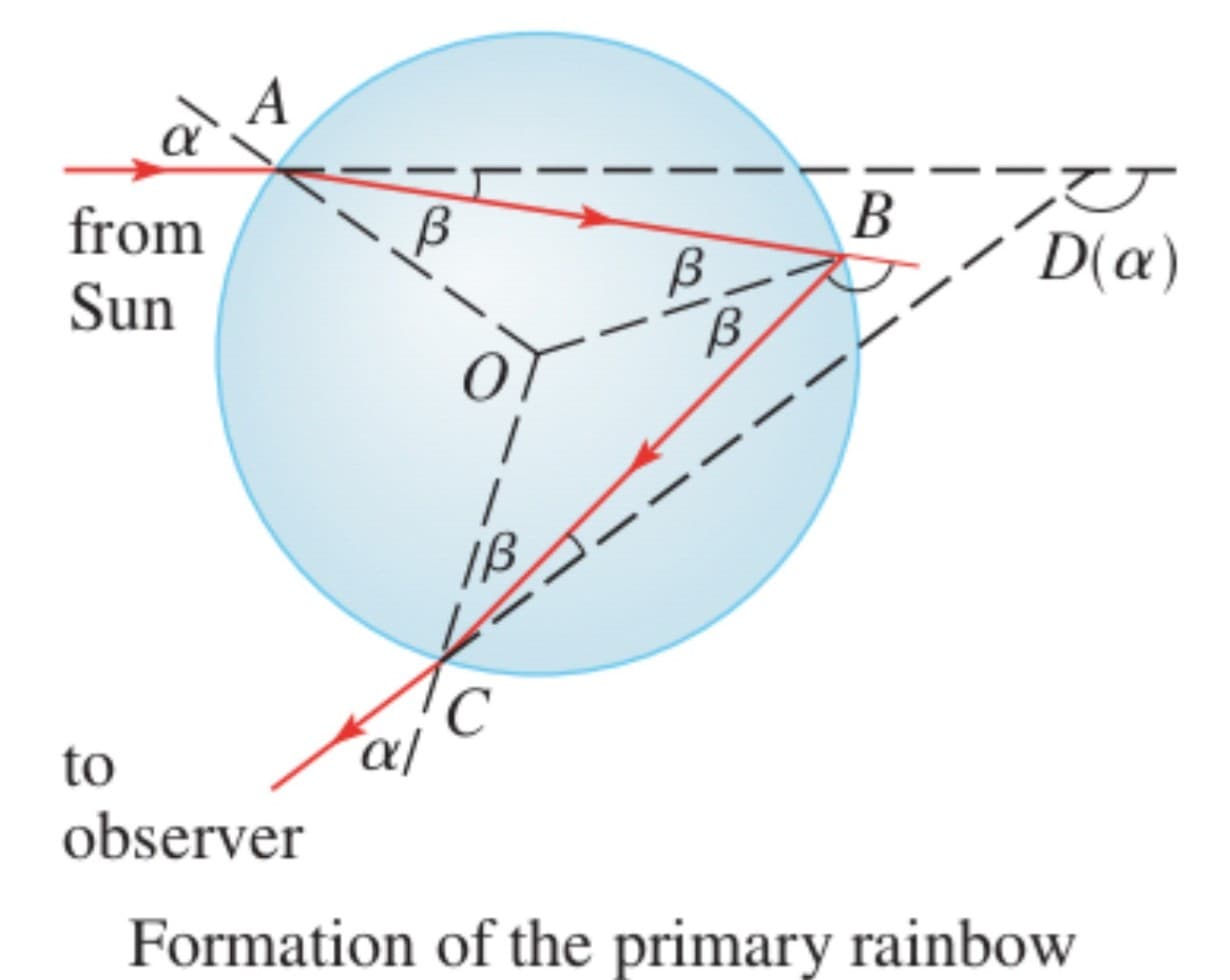
證明偏差角在 $\alpha\approx 59.4^{\circ}$ 時會有最小值 $\alpha\approx 59.4^{\circ}$。
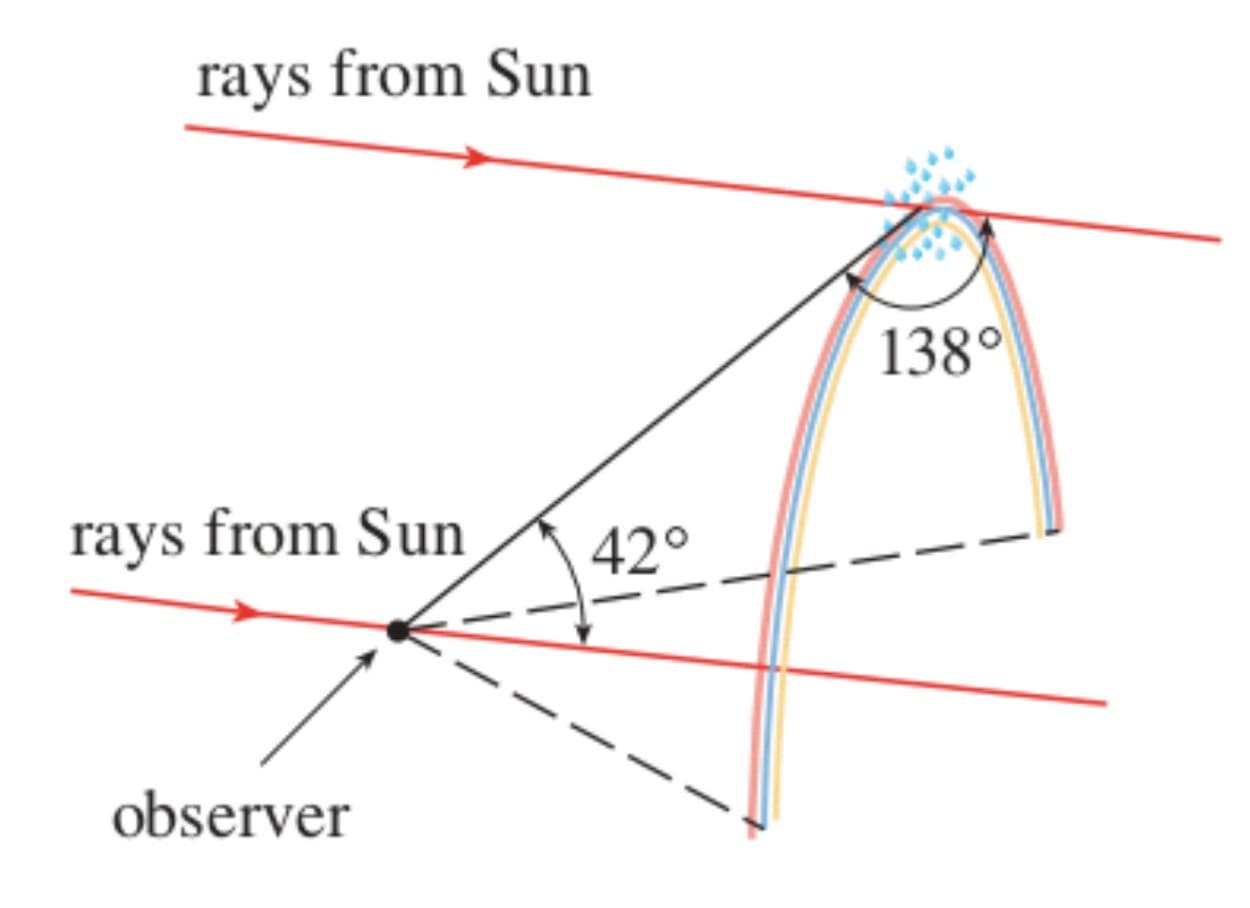
最小偏差角的意義是當$\alpha\approx 59.4^{\circ}$ 時,我們知道 $D’(\alpha)\approx 0$,則 $\frac{\Delta D}{\Delta \alpha}\approx 0$ 。這代表當很多光束在 $\alpha\approx 59.4^{\circ}$ 時偏差大約相同,而正是因為接近最小偏差方向的光線集中產生主彩虹的亮度。下面這張圖顯示了從觀察者到彩虹最高點的仰角為 $180^{\circ}- 138^{\circ} = 42^{\circ}$(這個角度就叫做彩虹角)。
問題二:
問題1解釋了主彩虹的位置,那我們要如何解釋顏色呢?陽光的波長範圍從紅色到橙色,黃色,綠色,藍色,靛藍和紫色。正如牛頓在1666年的棱鏡實驗中發現的那樣,每種顏色的折射率都不同(這種效果稱為色散)。紅光的折射率為 $k \approx 1.3318$,紫光的折射率為 $k\approx 1.3435$。透過對的這些值 $k$ 重複問題1的計算,證明紅色光道的彩虹角是 $42.3^{\circ}$ 而紫色光道的彩虹角是 $40.6^{\circ}$ 。因此,彩虹實際上是由對應於這七個顏色的七個單獨的光道組成的。
問題三:
或許你曾經看過主彩虹上較暗的次彩虹。這是由於光線進入雨滴並在A處折射、反射兩次(在B和C處)以及在D處離開雨滴而折射的那部分光束所致(如下圖)。這次偏差角$D(\alpha)$是射線在此四階段過程中經歷的逆時針旋轉的總量。
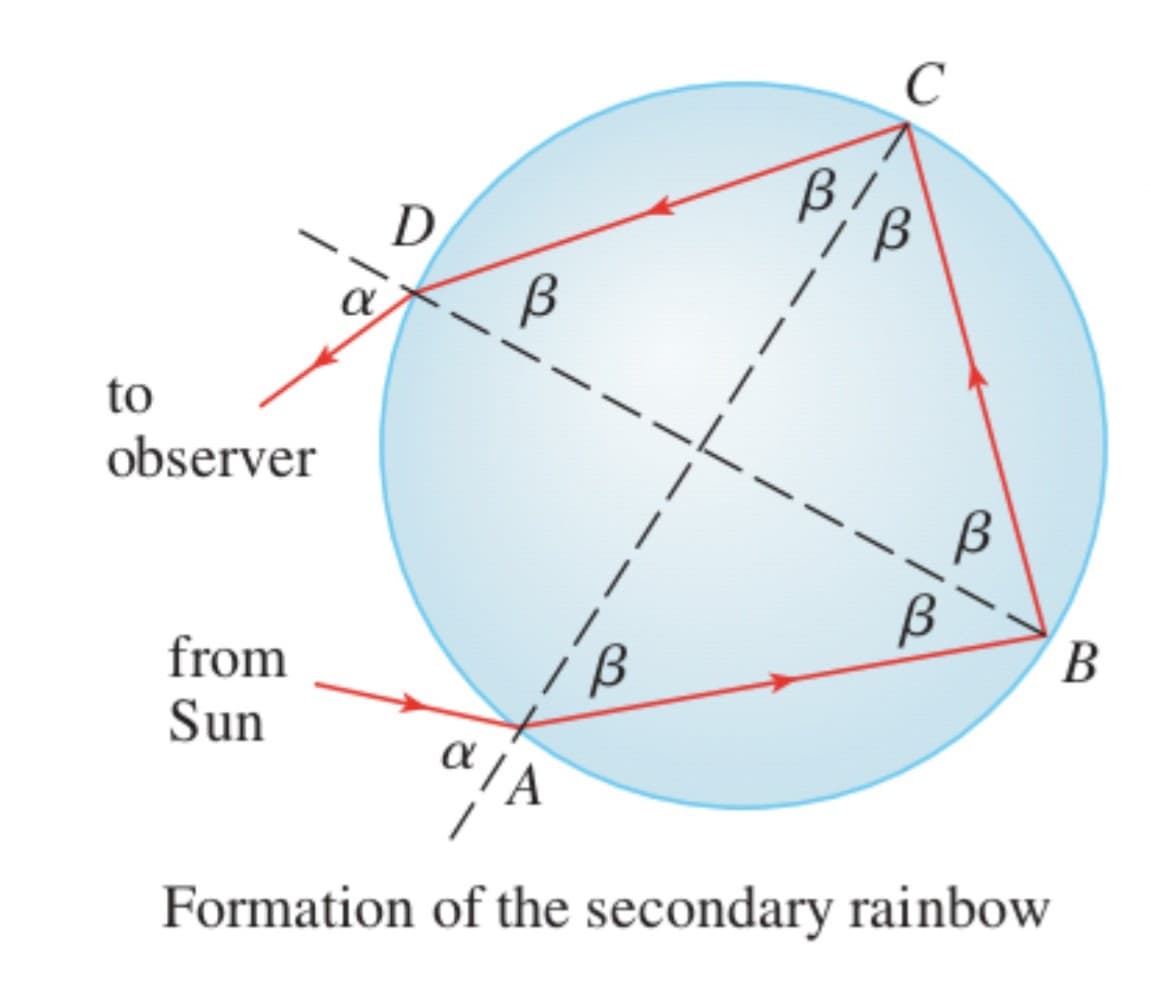
證明 $D(\alpha ) = 2\alpha - 6\beta + 2\pi$ 和 $D(\alpha)$ 在 $\cos\alpha = \sqrt\frac{k^2-1}{8}$ 時有最小值。
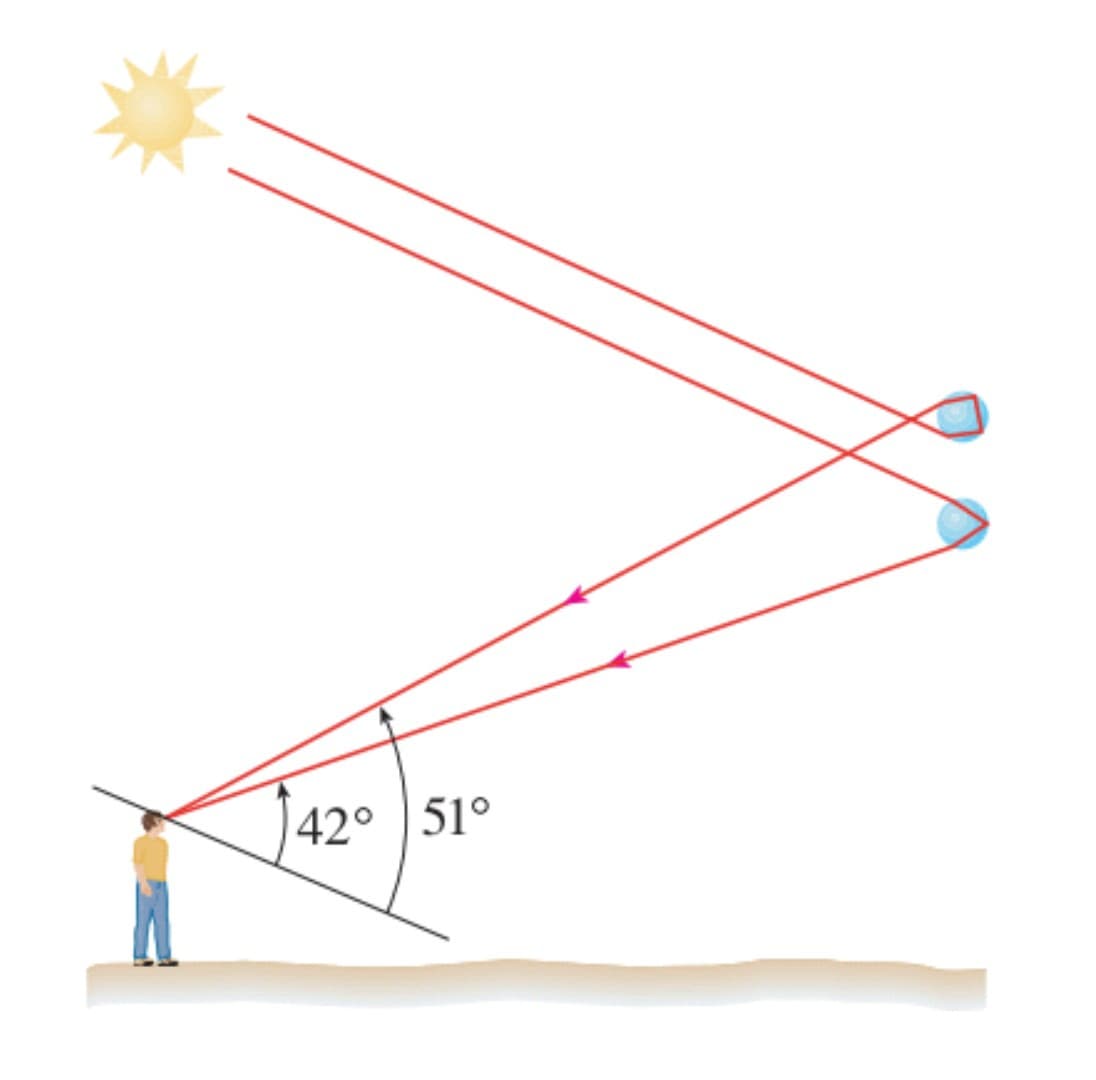
用 $k=\frac{4}{3}$ ,表示最小偏差角大約等於 $129^{\circ}$ 且次彩虹的彩虹角大約等於$51^{\circ}$ ,如下圖所示。
問題四:
證明次彩虹中的顏色以與主要彩虹中的顏色相反的順序顯現。