Sec.4.1 - The Calculus of ranbows
Applied Project in Sec.4.1, Calculus by Stewart
Chinese version: 彩虹的微積分學
Rainbows are created when raindrops scatter sunlight. They have fascinated mankind since ancient times and have inspired attempts at scientific explanation since the time of Aristotle. In this project we use the ideas of Descartes and Newton to explain the shape, location, and colors of rainbows.
Question 1:
The figure shows a ray of sunlight entering spherical raindrop at A. Some of the light is reflected, but the line AB shows the path of the part that enters the drop. Notice that the light is refracted toward the normal line AO and in fact Snell"s Law says that $\sin\alpha=k \sin\beta$, where $\alpha$ is the angle of incidence, $\beta$ is the angle of refraction, and $k\approx\frac{4}{3}$ is the index of refraction for water. At B some of the light passes through the drop and is refracted into the air, but the line BC shows the part that is reflected. (The angle of incidence equals the angle of reflection.) When the ray reaches C, part of it is reflected, but for the time being we are more interested in the part that leaves the raindrop at C.(Notice that it is refracted away from the normal line.) The angle of deviation $D(\alpha )$ is the amount of clockwise rotation that the ray has undergone during this three-stage process. Thus $$ D(\alpha ) = (\alpha - \beta ) + (\pi - 2\beta ) + (\alpha - \beta) = \pi + 2\alpha - 4\beta. $$
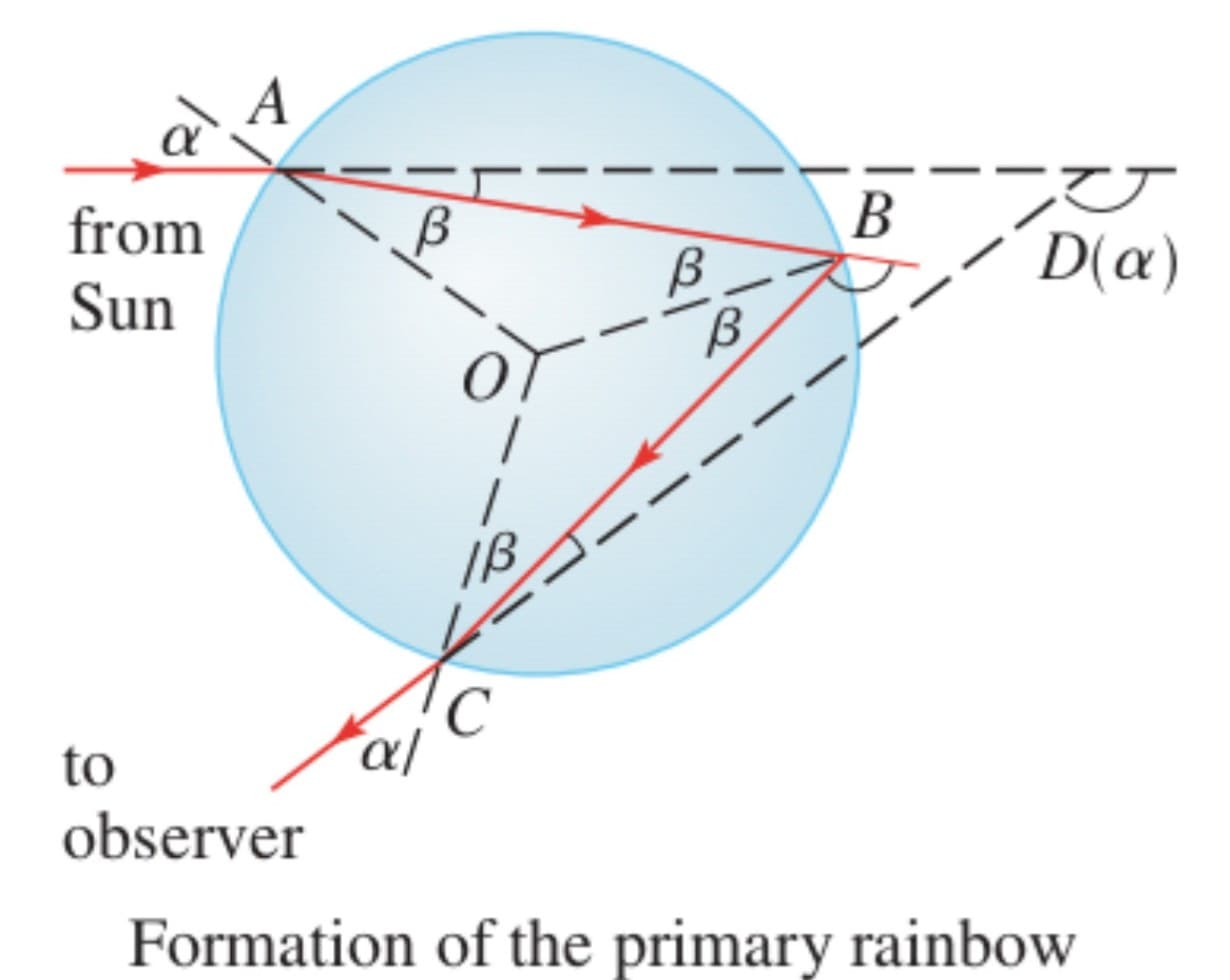
Show that the minimum value of deviation is $D(\alpha)\approx 138^{\circ}$; and occurs when $\alpha\approx 59.4^{\circ}$.
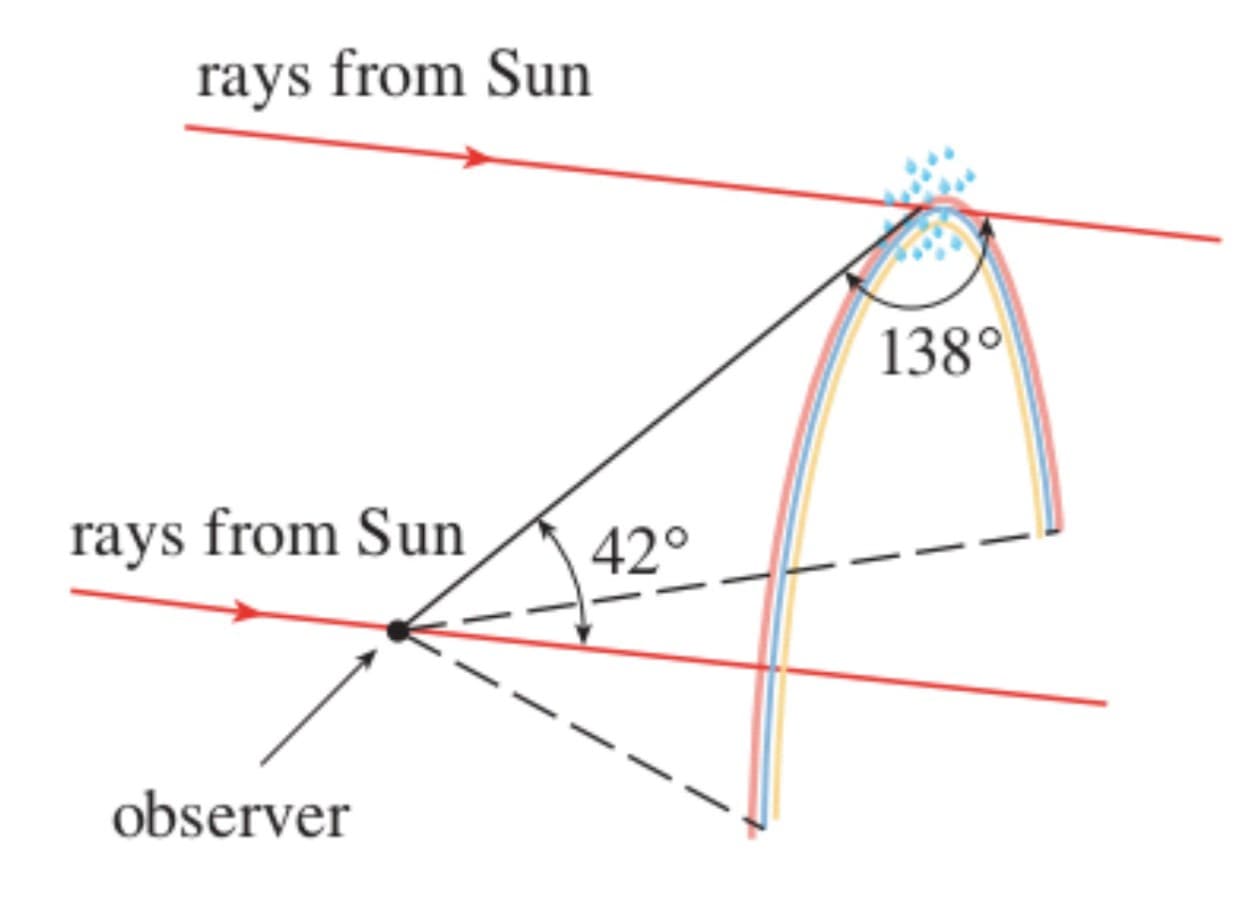
The significance of the minimum deviation is that when $\alpha\approx 59.4^{\circ}$ we have $D'(\alpha)\approx 0$, so $\frac{\Delta D}{\Delta \alpha}\approx 0.$ This means that many rays with $\alpha\approx 59.4^{\circ}$ become deviated by approximately the same amount. It it the concentration of rays coming from near the direction of minimum deviation that creates the brightness of the primary rainbow. The figure at the left shows that the angle of elevation from the observer up to the highest point on the rainbow is $180^{\circ}- 138^{\circ} = 42^{\circ}$. (This angle is called the rainbow angle .)
Question 2:
Problem 1 explains the location of the primary rainbow, but how do we explain the colors? Sunlight comprises a range of wavelengths, from the red range through orange, yellow, green, blue, indigo, and violet. As Newton discovered in his prism experiments of 1666, the index of refraction is different for each color, (The effect is called dispersion.) For red light the refractive index $k \approx 1.3318$, whereas for violet light it is $k\approx 1.3435$. By repeating the calculation of Problem 1 for these values of $k$, show that the rainbow angle is about $42.3^{\circ}$ for red bow and $40.6^{\circ}$ for the violet bow. So the rainbow really consists of seven individual bows corresponding to the seven colors.
Question 3:
Perhaps you have seen a fainter secondary rainbow above the primary bow. That results from the part of a ray that enters a raindrop and is refracted at A, reflected twice (at B and C), and refracted as it leaves the drop at D (see the figure at the left). This time the deviation angle $D(\alpha)$ is the total amount of counterclockwise rotation that the ray undergoes in this four-stage process.
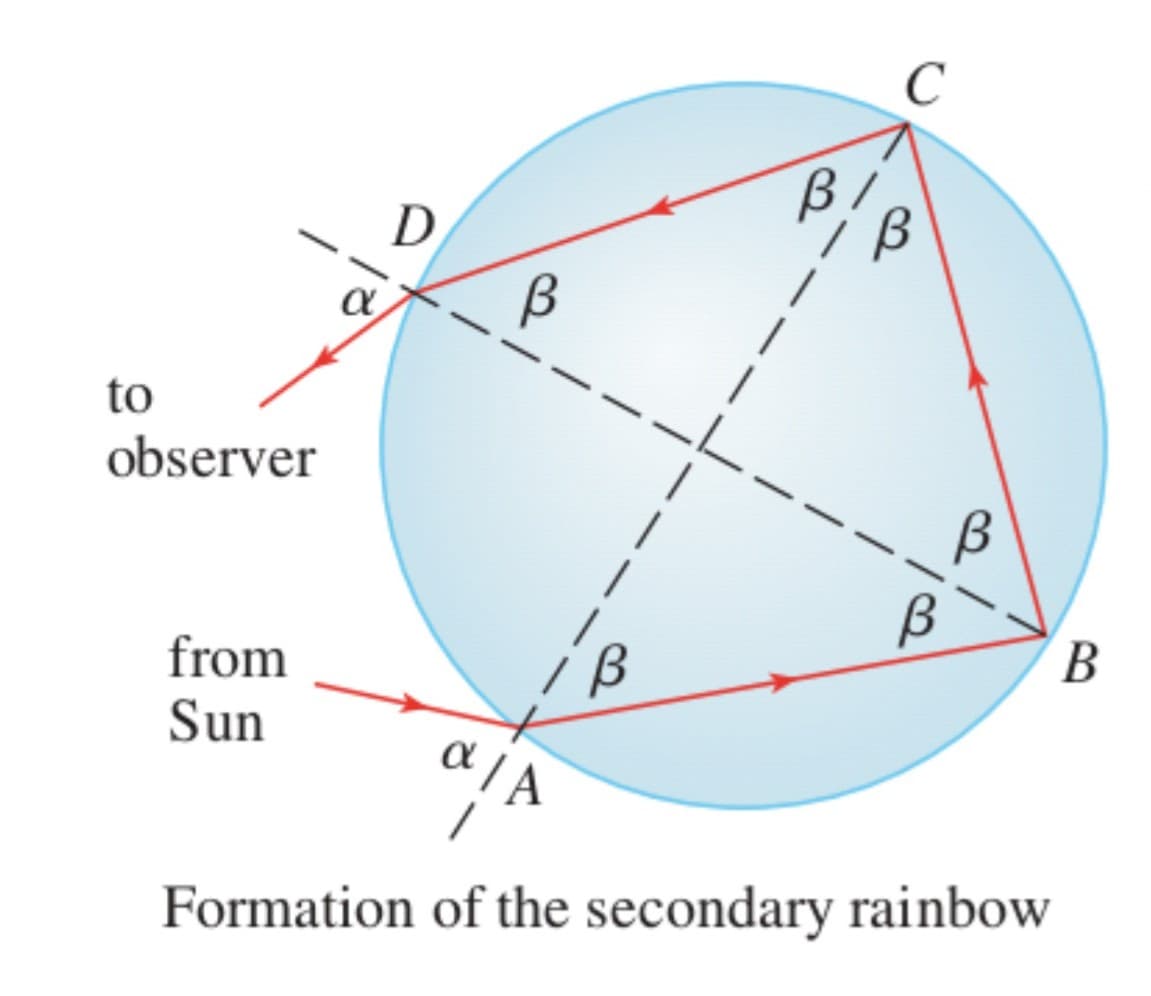
Show that $D(\alpha ) = 2\alpha - 6\beta + 2\pi$ and $D(\alpha)$ has a minimum value when $\cos\alpha = \sqrt\frac{k^2-1}{8}$.
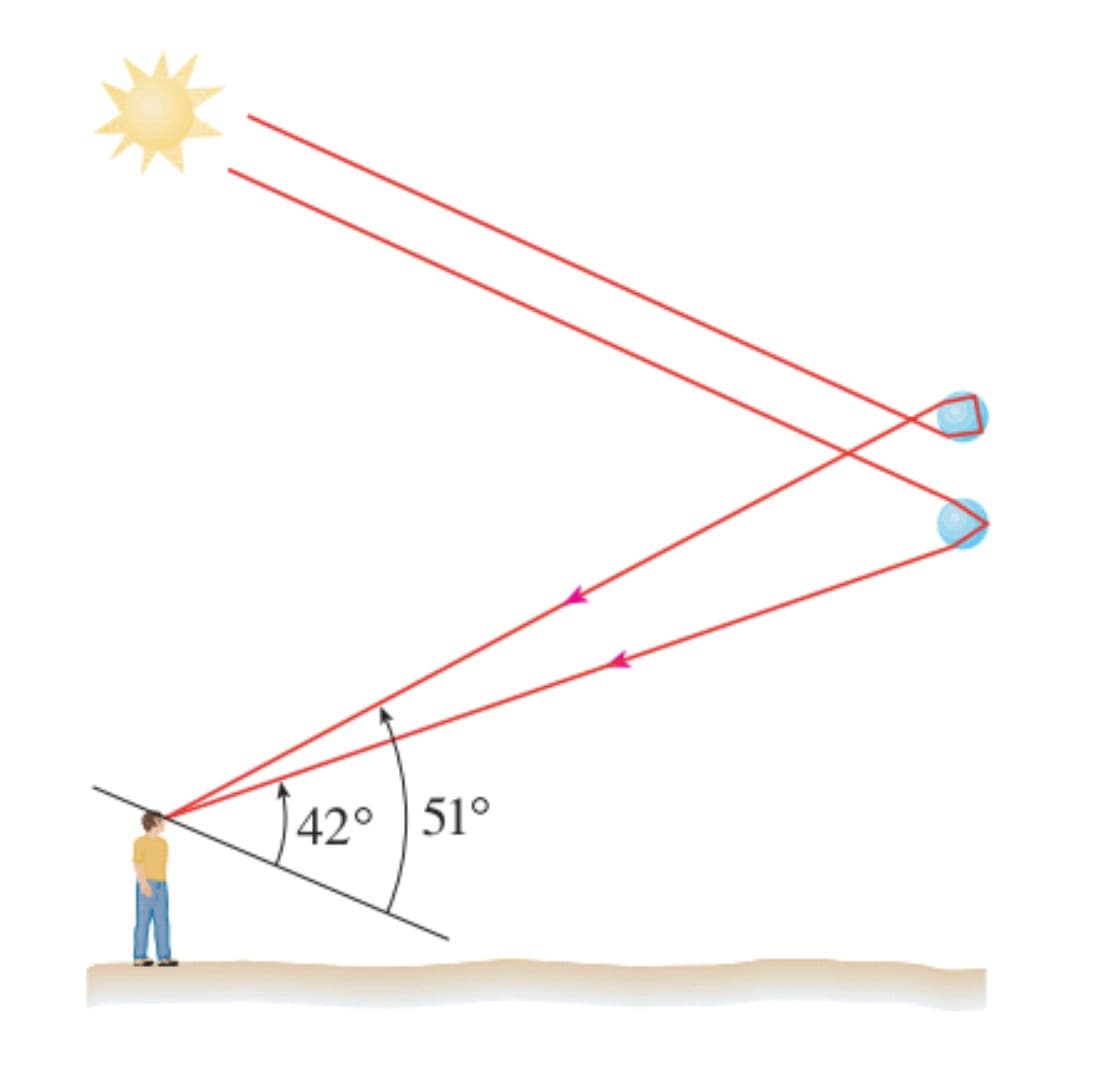
Taking $k=\frac{4}{3}$, show that the minimum deviation is about $129^{\circ}$ and so the rainbow angle for the secondary rainbow is about $51^{\circ}$, as shown in the figure below.
Question 4:
Show that the colors in the secondary rainbow appear in the opposite order from those in the primary rainbow.