Sec.4.7 - 罐頭的形狀

Applied Project 1 in Sec.4.7, Calculus by Stewart
英文版請見 The shape of a can

給定一個體積為 $v$ 的圓柱體罐頭，我們想找到一個高 $h$ 和半徑 $r$ ，將製成罐頭的金屬量減到最小。

如果我們將製程中金屬的浪費忽略，那麼這個問題就是在找圓柱的最小表面積。計算之後發現這個問題的解是 $h=2r$ ，也就是說，高必須相等於直徑。

然而，去超市晃晃會發現一般而言市面上的罐頭的高都大於直徑， $h/r$ 的比例可以從 $2$ 到大約 $3.8$。讓我們來看看是否可以解釋這個現象。

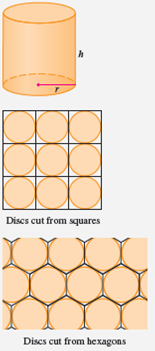
問題 1: 罐頭的原料是從金屬板上切割下來的，它(圓柱)的邊是由彎曲的矩形組成，而這些矩形也是從板上切成且過程中幾乎沒有浪費。

然而，如果圓柱上下的圓面是由邊為 $2r$ 的正方形切割的，那麼一定會有大量的金屬浪費，儘管它可以回收再利用，但對罐頭製造商來說是幾乎沒有任何價值的。

因此，如果是這樣的話，我們就需要找到一組 $h/r$ 比例來最小化金屬的使用。

答案:

$$ \frac{h}{r} = \frac{8}{\pi}\approx 2.55 $$

問題 2: 若將金屬板劃分為六邊形並從六邊形切下圓形的蓋子和底座，可以更有效地填充圓盤。如果採用這個方法，要找到能讓使用的金屬量最小化的 $h/r$ 的比例。

答案:

$$ \frac{h}{r} = \frac{4\sqrt{3}}{\pi}\approx 2.21 $$

問題 3: 除了罐子本身的金屬材料，我們現在將製程中所需成本包含進去

• 假設大部分的成本發生在黏接邊與邊的地方

製作一圓柱罐，首先我們彎曲一矩形並將邊與邊黏接在一起以製成圓柱殼（高度為 $ h $）；接著，將兩個圓盤與圓柱殼黏接（圓盤長度為$2πr$）。 由上可知，黏接成本為 $ k(h+4πr) $， $k$ 為單位面積金屬成本可黏接長度的倒數。

同問題二，圓盤由一正六邊形切割而成，所以總成本包括金屬成本和黏接的成本，與$4\sqrt{3}r^2 + 2\pi r h + k(4\pi r + h) $成正比。

答案：

發生最小值時圓柱體的高度與半徑比為: $$ \frac{h}{r} = \frac{4\sqrt{3}r + 2k\pi}{\pi r + k} $$

問題 4: 當圓柱罐非常大且黏接的成本低時結果會是怎樣呢？反之圓柱罐非常小且黏接的成本高？

答案:

對固定體積的圓柱體而言

• 當黏接成本低 $0 < k ≪ 1$時，

$$ \frac{h}{r} = \frac{4\sqrt{3}r + 2k\pi}{\pi r + k} \to \frac{4\sqrt{3}}{\pi}\approx 2.21 $$

• 當黏接成本較高 $ k ≫ 1$ 時，

$$ \frac{h}{r} = \frac{4\sqrt{3}r + 2k\pi}{\pi r + k} \to 2\pi\approx 6.28 $$

如果$ k $為定值，我們先找出體積 $ v $與比值 $h/r$ 的關係。為了書寫方便，我們定義 $R = h/r$ 。接著重新將$ r$表示為 $v$與 $R$ 的函數， $$ r = \sqrt[3]{\frac{v}{\pi R}} $$ 經過運算 $$ \frac{\sqrt[3]{v}}{k} = \frac{\sqrt[3]{\pi R}(2\pi - R)}{\pi R - 4\sqrt{3}} $$

• 當圓柱罐非常大 $v ≫ 1$ 時，右式的分母趨近於 0，

$$ \pi R - 4\sqrt{3} \to 0 \Longrightarrow \frac{h}{r} = R \to \frac{4\sqrt{3}}{\pi}\approx 2.21 $$

• 當圓柱罐非常較小 $0 < v ≪ 1$ 時，右式分子趨近於 0， $$ 2\pi - R \to 0 \Longrightarrow \frac{h}{r} = R \to 2\pi\approx 6.28 $$