Sec.3.10 - Taylor polynomials

Laboratory Project in Sec.3.10, Calculus by Stewart
Chinese version: 泰勒級數

The tangent line approximation $L(x)$ is the best first-degree (linear) approximation to $f(x)$ near $x=a$ because $f(x)$ and $L(x)$ have the same rate of change (derivative) at $x=a$. For a better approximation than a linear one, let’s try a second-degree (quadratic) approximation $P(x)$. In other words, we approximate a curve by a parabola instead of a straight line. To make sure that the approximation is a good one, we stipulate the following:

1. $P$ and $f$ should have the same value at $a$. ($P(a)=f(a)$)
2. $P$ and $f$ should have the same rate of change at $a$. ($P’(a)=f’(a)$)
3. The slopes of $P$ and $f$ should change at the same rate at $a$. ($P’'(a)=f’'(a)$)

---

Question 1： Find the quadratic approximation $P(x)=A+Bx+Cx^{2}$ to the function $f(x)=cosx$ that satisfies conditions (i), (ii),and (iii) with $a=0$ . Graph $P$, $f$ and the linear approximation $L(x)=1$ on a common screen. Comment on how well the functions $P$ and $L$ approximate $f$.

Answer:

$P(x)=1-\frac{1}{2}x^{2}$, and the graph shows:

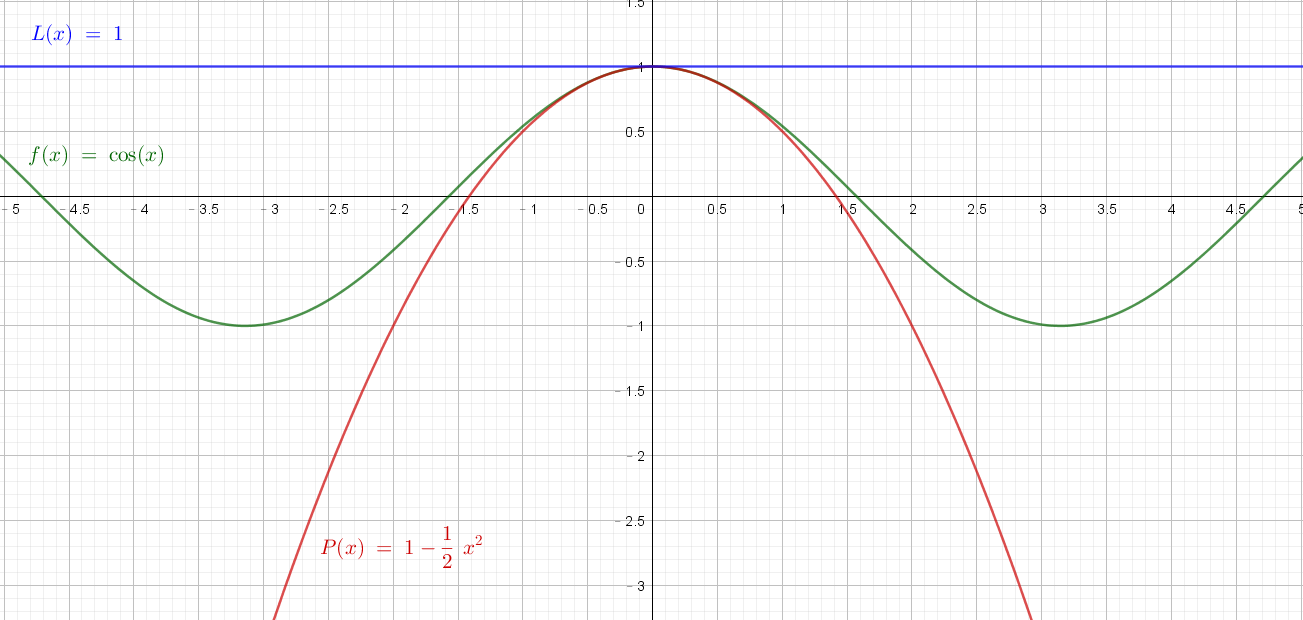
According to the graph, when $x\rightarrow a$, $|P(x)-f(x)|$ «$|L(x)-f(x)|$, therefore quadratic approximation $P(x)$ serves as a better approximation than linear approximation $L(x)$ to $f(x)$ near $x=0$ .

---

Question 2： Determine the values of $x$ for which the quadratic approximation $f(x)\approx P(x)$ in Problem 1 is accurate to within $0.1$.

Answer:

We draw the graph of $g(x),P(x),h(x)$:

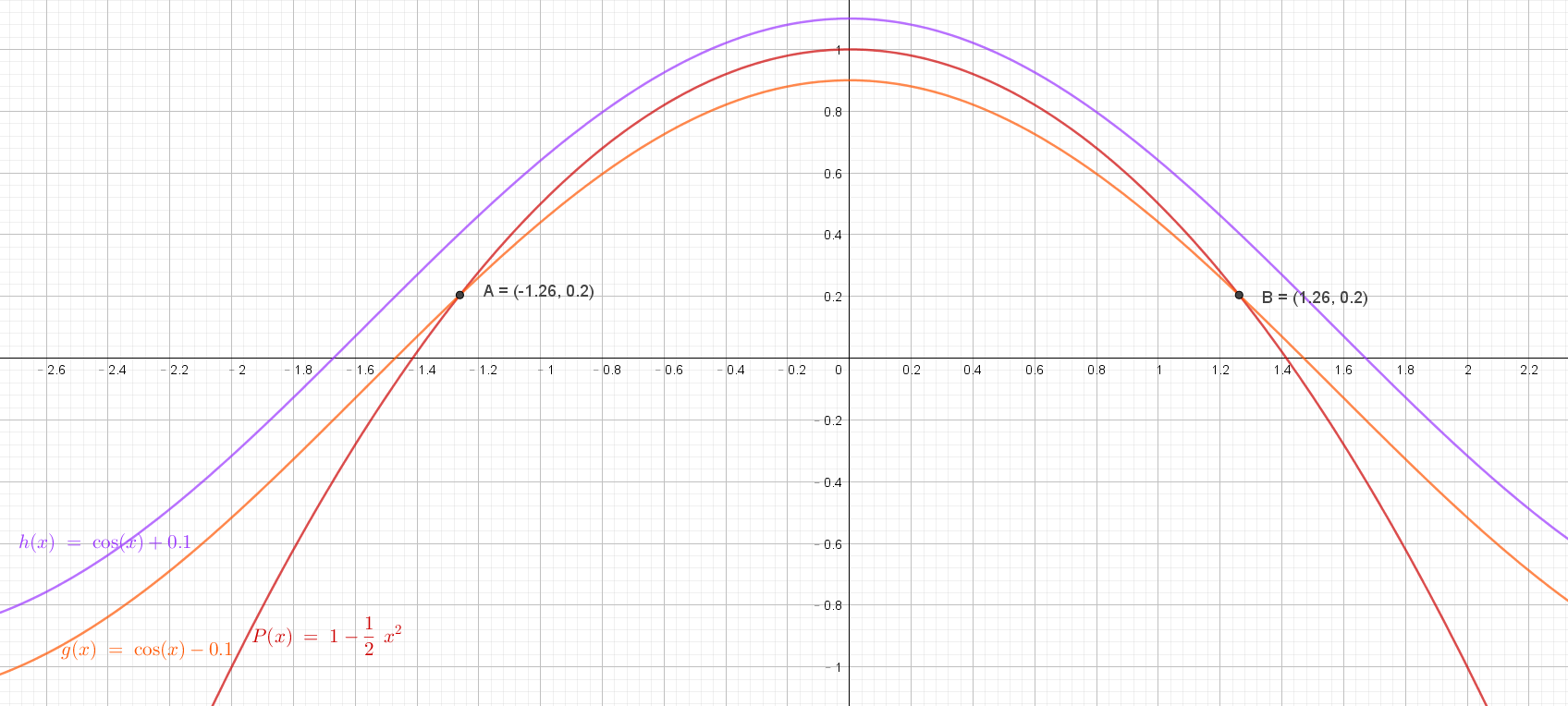
According to the graph, when $-1.26\leq x\leq 1.26$, it satisfies $|P(x)-f(x)|\leq 0.1$.

---

Question 3： To approximate a function $f$ by a quadratic function $P$ near a number $a$, it is best to write $P$ in the form $$ P(x)=A+B(x-a)+C(x-a)^{2}。 $$ Show that the quadratic function that satisfies conditions (i), (ii), and (iii) is $$ P(x)=f(a)+f’(a)(x-a)+\frac{1}{2} f’'(a)(x-a)^{2}。 $$

Answer:

$$ P(x)=f(a)+f’(a)(x-a)+\frac{1}{2} f’'(a)(x-a)^{2}. $$

---

Question 4: Find the quadratic approximation to $F(x)=\sqrt{x+3}\quad$ near $a=1$. Graph $f$, the quadratic approximation, and the linear approximation from Example 3.10.2 on a common screen. What do you conclude?

Answer:

We draw the graph of $f(x),P(x)$ and the linear approximation from Example 3.10.2：

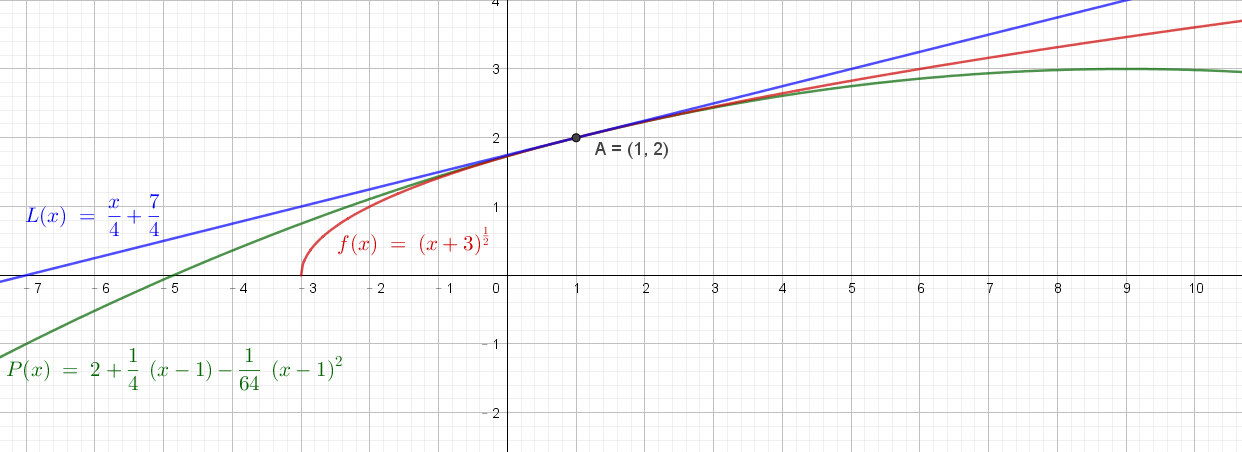
According to the graph, when $x\rightarrow 1$, quadratic approximation $P(x)$ serves as a better approximation than linear approximation $L(x)$.

---

Question 5: Instead of being satisfied with a linear or quadratic approximation to $f(x)$ near $x=a$, let’s try to find better approximations with higher-degree polynomials. We look for an nth-degree polynomial $$ T_{n}(x)=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+c_{3}(x-a)^{3}+…+c_{n}(x-a)^{n}， $$ which satisfies when $x=a$, $$ T_{n}^{(k)}(a)=f^{(k)}(a), \quad k=1, \cdots, n。 $$ Show that these conditions are satisfied if $c_{k}=\frac{f^{(k)}(a)}{k!}$.

The resulting polynomial: $$ T_{n}(x)=f(a)+f’(a)(x-a)+\frac{f’'(a)}{2!} (x-a)^{2}+…+\frac{f^{(n)}(a)}{n!}(x-a)^{n}。 $$ is called the nth-degree Taylor polynomial of $f$ centered at $a$.

---

Question 6: Find the 8th-degree Taylor polynomial centered at $a=0$ for the function $f(x)=\cos x$. Graph $f$ together with the Taylor polynomials $T_{2},T_{4},T_{6},T_{8}$ in the viewing rectangle $x=[-5,5]$ by $y=[-1.4,1.4]$ and comment how well they approximate $f$.

Answer:

We draw the graph of$f$ and $T_{2},T_{4},T_{6},T_{8}$, and the rectangle $x=[-5,5]$ by $y=[-1.4,1.4]$

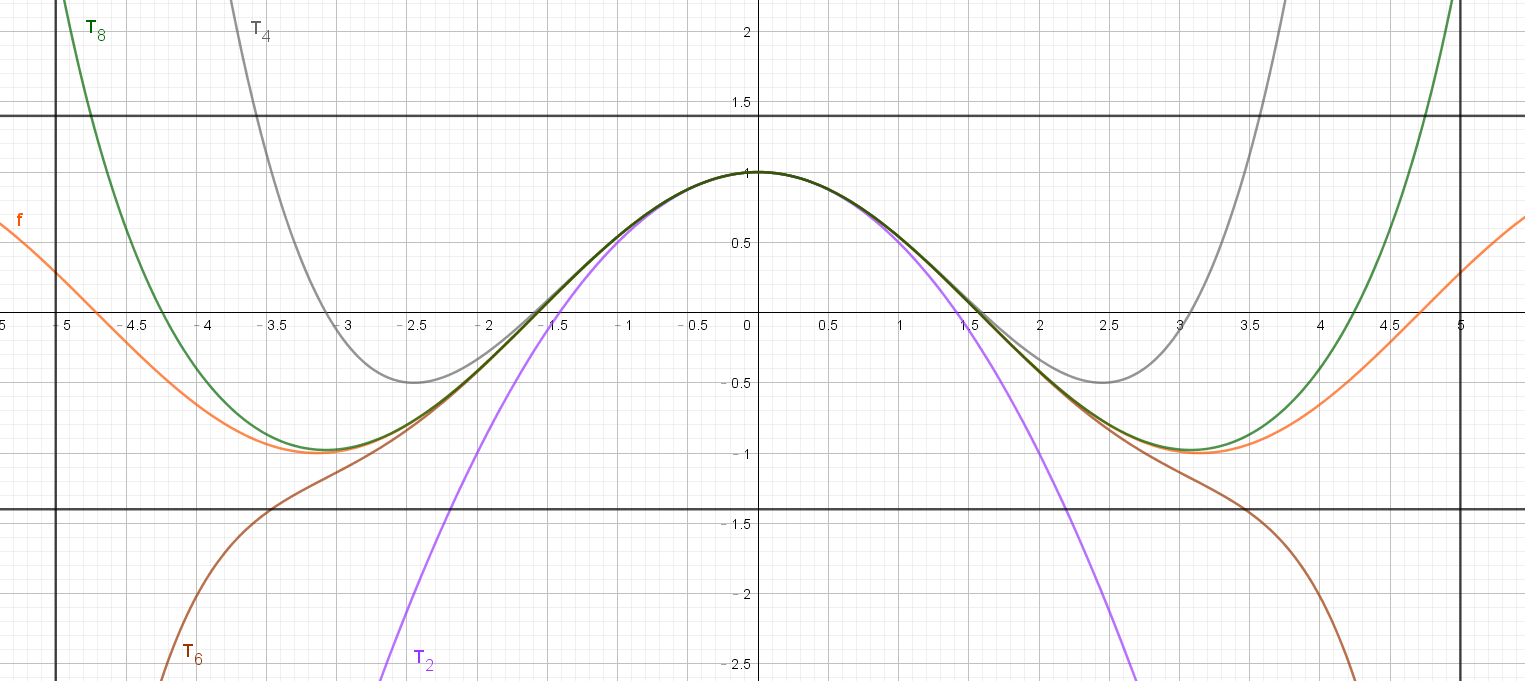
According to the graph, at $a=0$, when the degree of approximation $T$ goes higher, the approximation is more similar to $f$ , and the interval for approximation becomes larger, that is, within four approximation $T$, function $T_{8}$ serves as the best approximation for $f$ at $a=0$.

---