Sec.3.10 - 泰勒級數
Laboratory Project in Sec.3.10, Calculus by Stewart
英文版請見 Taylor polynomials
在近似函數 $f(x)$ 在 $x=a$ 的值時,切線逼近函數(tangent line approximation) $L(x)$ 是線性逼近(linear approximation)中最好的近似方式,這是因為 $f(x)$ 及 $L(x)$ 在 $x=a$ 這點有相同的改變速率。
為了找尋比線性逼近更好的近似方式,我們嘗試利用二次逼近函數(quadratic approximation) $Q(x)$ 來做近似,換句話說,我們利用拋物線來逼近 $f(x)$ 的值而非直線。為了確定這樣的近似方式是合理的,我們規定以下條件:
- $P(a)=f(a)$
- $P’(a)=f’(a)$
- $P’'(a)=f’'(a)$
問題 1: 對於函數 $f(x)=\cos(x)$,找尋它在 $a=0$ 時的二次逼近函數 $P(x)=A+Bx+Cx^2$,並且此函數須滿足上述介紹中的三個條件。接著對函數 $P,f$ 及線性逼近函數 $L(x)=1$ 作圖,比較 $P$ 和 $f$ 哪一個逼近函數比較精確。
解:
$P(x)=1-\frac{1}{2}x^{2}$
函數 $P,f$ 及線性逼近函數 $L(x)=1$ 作圖如下:
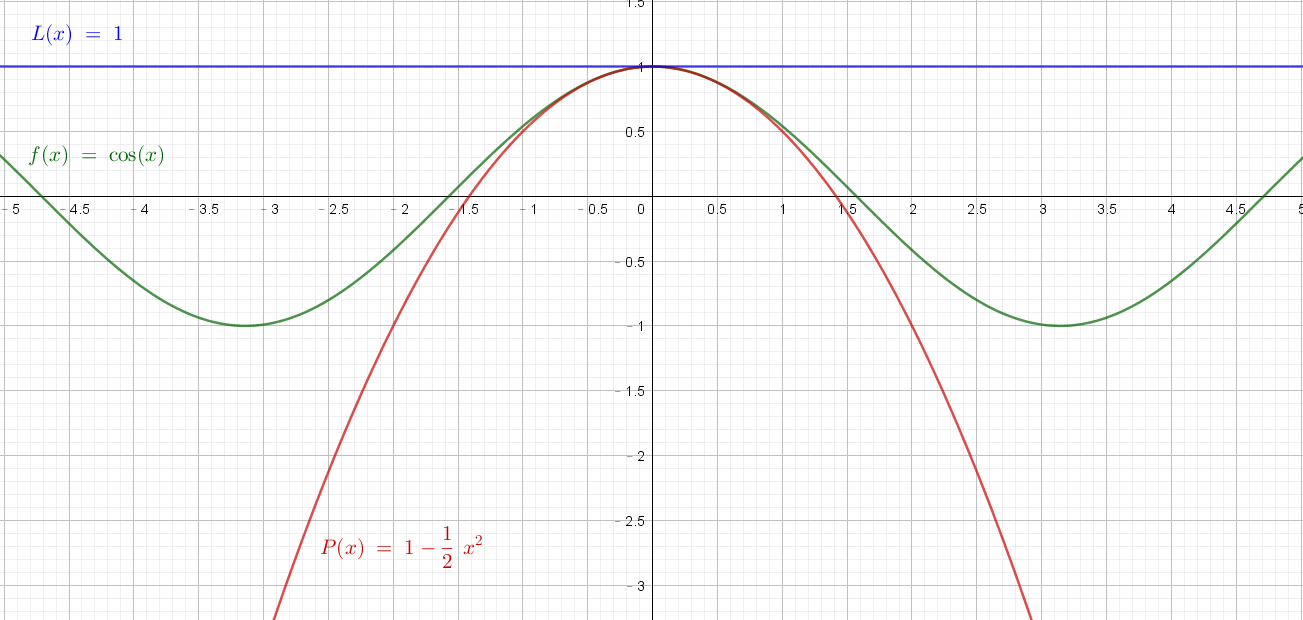
由上圖可知,在 $x\rightarrow a$ 時,$|P(x)-f(x)|«|L(x)-f(x)|$,因此二次逼近函數 $P(x)$ 近似函數 $f(x)$ 的程度較優於線性逼近函數 $L(x)$。
問題 2: 延續題1,試求符合條件的 $x$ 滿足 $P(x)$ 及 $f(x)$ 的差值在 $0.1$ 內。
解:
對 $g(x),P(x),h(x)$ 作圖如下:
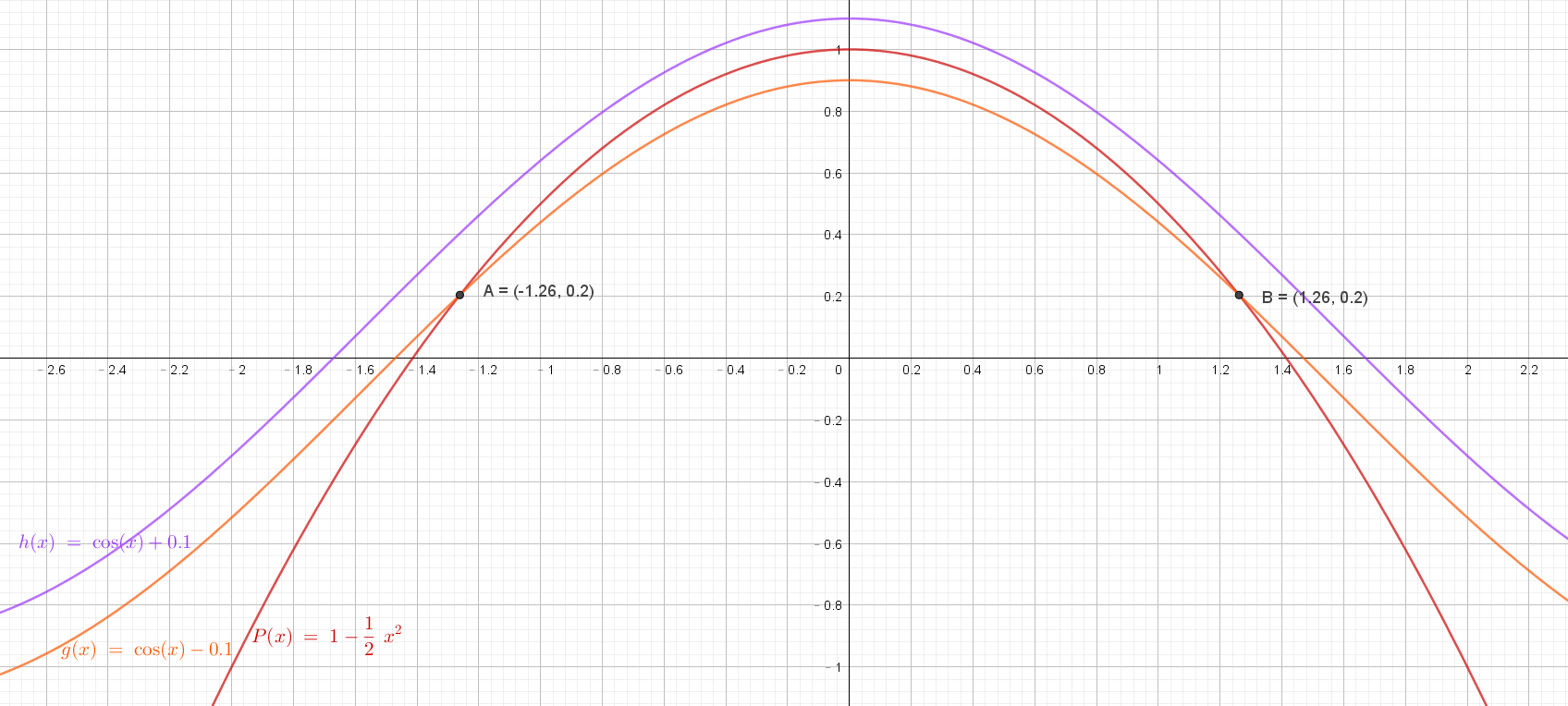
由圖可知,在 $-1.26\leq x\leq 1.26$ 時,滿足 $|P(x)-f(x)|\leq 0.1$。
問題 3: 利用二次逼近函數 $P$ 來近似在 $x=a$ 附近的函數 $f$ 時,可以先將函數 $P$ 寫成以下形式: $$ P(x)=A+B(x-a)+C(x-a)^{2}。 $$ 證明一個滿足專題介紹中3個條件的二次逼近函數$P(x)$可以表示為 $$ P(x)=f(a)+f’(a)(x-a)+\frac{1}{2} f’'(a)(x-a)^{2}。 $$
解:
$$ P(x)=f(a)+f’(a)(x-a)+\frac{1}{2} f’'(a)(x-a)^{2}。 $$
問題 4: 找尋函數 $f(x)=\sqrt{x+3}$ 在 $a=1$ 時的二次逼近函數,接著對 $f$、二次逼近函數及線性逼近函數做圖。你能做怎樣的結論?
解:
對函數 $f(x),P(x)$ 及線性逼近函數作圖如下:
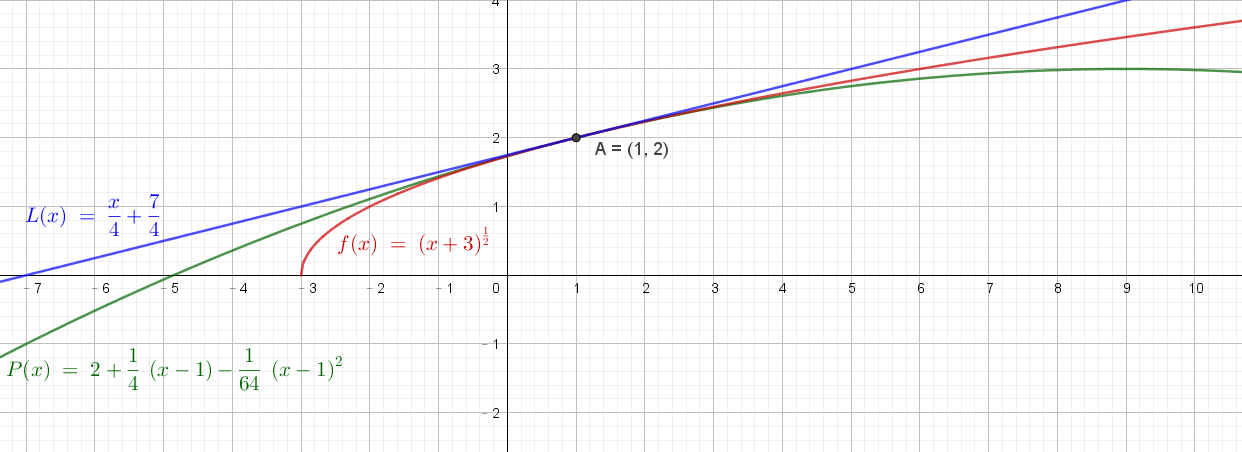
由圖可知,在 $x\rightarrow 1$ 的地方,二次逼近函數 $P(x)$ 的近似程度較線性逼近函數 $L(x)$ 還要精確。
問題 5: 對於函數 $f(x)$,在 $x\to a$ 的近似方式除了用二次逼近函數或線性逼近函數外,我們試著找尋更精確的多次逼近函數。考慮一個 $n$ 次多項式: $$ T_{n}(x)=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+c_{3}(x-a)^{3}+…+c_{n}(x-a)^{n}, $$ 它滿足在 $x=a$ 時, $$ T_{n}^{(k)}(a)=f^{(k)}(a), \quad k=1, \cdots, n。 $$ 證明:滿足上述條件的 $T_{n}(x)$ 其係數 $c_{k}=\frac{f^{(k)}(a)}{k!}$。(將係數 $c_{k}$ 代入函數 $T_{n}(x)$ 後,函數為 $$ T_{n}(x)=f(a)+f’(a)(x-a)+\frac{f’'(a)}{2!} (x-a)^{2}+…+\frac{f^{(n)}(a)}{n!}(x-a)^{n}。 $$ 此即為函數 $f$ 在點 $a$ 的 $n$ 階泰勒級數。)
問題 6: 試求函數 $f(x)=\cos(x)$ 在點 $a=0$ 的8階泰勒級數。除此之外,對函數 $f$ 及 $T_{2},T_{4},T_{6},T_{8}$ 做圖,考慮範圍為 $x=[-5,5],y=[-1.4,1.4]$ 之長方形,評論對於函數 $f$,4條逼近函數 $T$ 的近似程度。
解:
對函數 $f$ 及 $T_{2},T_{4},T_{6},T_{8}$ 做圖,黑色框線為題目要求 $x=[-5,5],y=[-1.4,1.4]$ 之長方形。
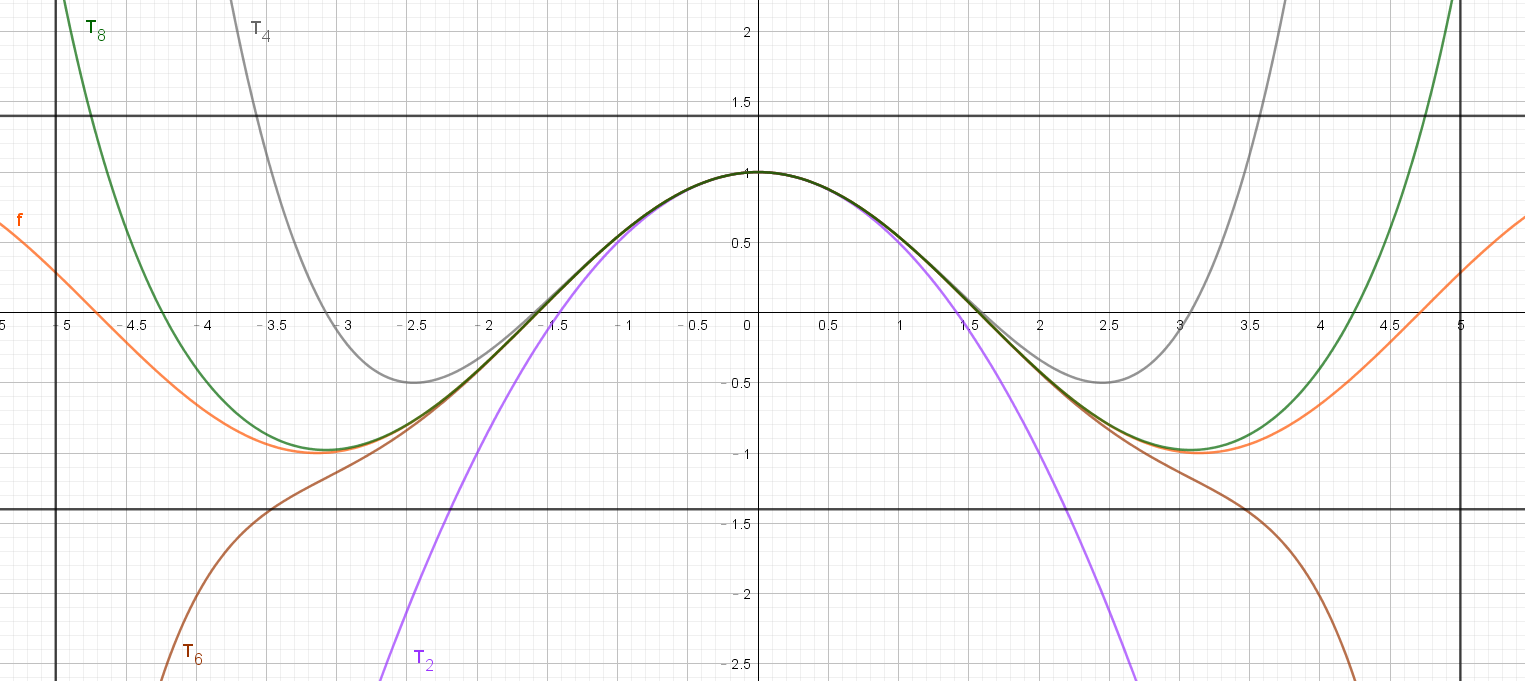
由圖可以看出逼近函數 $T$ 的次方越高,與函數 $f$ 在 $a=0$ 這點的相似程度就越高、範圍也越大。也就是說,在這4條函數中,對於函數 $f$ 在 $a=0$ 時的逼近函數以 $T_{8}(x)$ 最為精確。