Sec.14.4 - 速比濤鯊魚皮系列第四代泳裝

Applied Project in Sec.14.4, Calculus by Stewart
英文版請見 The speedo LZR razer

在體育運動中, 許多科技的進步讓運動員的表現更好. 最廣為人知的例子之一就是速比濤在2008年時推出鯊魚皮系列第四代泳裝, 宣稱這個連身泳衣可以減少泳者在水中的阻力. 圖1 顯示1990年到2011年男性和女性在長程自由式的賽事中打破世界紀錄的數量, 可以發現在2008年時數量大大的增加, 恰好是那款泳衣推出的時候, 這讓大家覺得這種泳衣根本就是一種科技的「禁藥」, 結果2010年以後所有的連身泳衣在競賽中都被禁止使用.

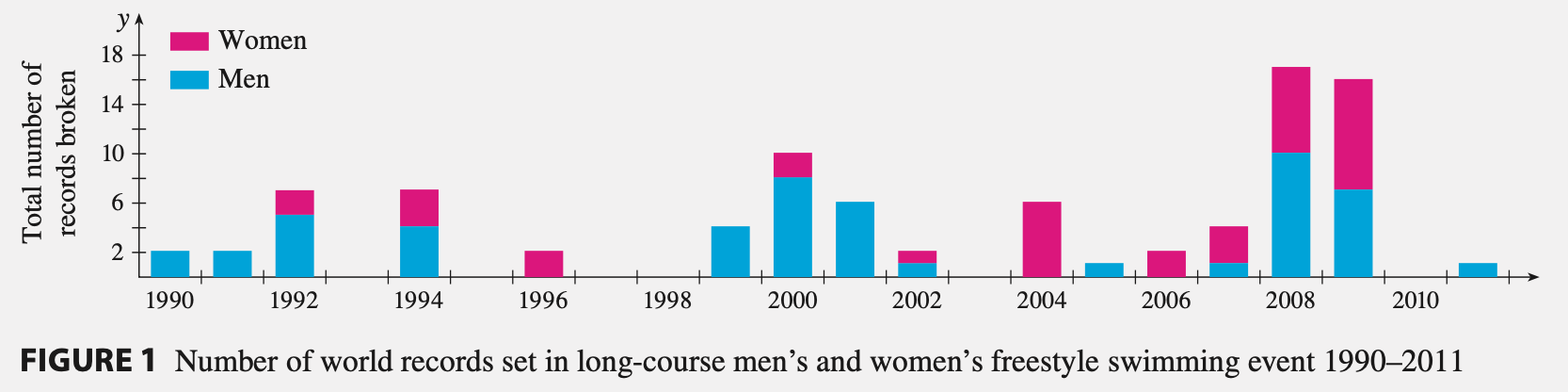
可能會讓人驚訝的是純粹減少阻力竟然可以在表現上有這麼大的影響力! 我們可以藉由簡單的數學模型更深入的探討這個現象.

在水中物體被驅動的速率 $v$ 公式如下 $$ v(P,C)=\left( \frac{2P}{kC}\right)^{\frac{1}{3}}, $$ 其中 $P$ 代表驅動物體所使用的功率, $C$ 是阻力係數, $k$ 是一個大於零的定值. 因此, 運動員可以藉由增加功率或是減少阻力係數來增加游泳速率, 但是這兩個因素影響速率的效果如何呢?

為了比較「增加功率」和「減少阻力」的影響, 我們需要以某種方式在共同的單位下比較兩者的差異. 最常見的方法就是給定一個功率或是阻力的百分比變化率, 測定速率隨之改變多少百分比.

若我們以分數的形式代表百分比, 則當功率被改變 $x$ 的比例後($x$對應到 $100x$), $P$ 會變化成 $P + xP$. 同理, 若阻力係數被改變 $y$ 的比例, $C$ 會變化成 $C + yC$. 最後, 這兩個因素造成的速率比例的改變為: $$ f(x,y)=\frac{v(P+xP,C+yC)-v(P,C)}{v(P,C)}. $$

問題 1:

函數 $f$ 代表功率的改變比例 $x$ 和阻力的改變比例 $y$ 所造成的速率改變比例, 請說明這個函數可以簡化成 $$ f(x,y)=\left(\frac{1+x}{1+y}\right)^{\frac{1}{3}}-1 $$ 由文字給定的敘述中, 請問函數 $f$ 的定義域為何?

解

$f$ 的定義域為 $$ \{ (x,y)\mid x\geq-1,\quad y>-1 \} $$

問題 2:

假設功率的改變比例 $x$ 和阻力的改變比例 $y$ 很小, 找出 $f(x, y)$ 的線性近似. 請問這個近似告訴你關於「增加功率」和「減少阻力」的影響存在哪些差異?

解

• 比較「增加功率」和「減少阻力」的影響

  根據函數 $f$ 線性逼近的結果, 增加功率 $x$ 或減少阻力 $y$ 所造成速率的增加比例都是三分之一. 因此, 對於速率的增加比例而言, 少量增加功率抑或是少量減少阻力所造成的影響並沒有差異.

問題 3:

計算 $f_{xx}(x, y)$ 和 $f_{yy}(x, y)$. 根據這些導數的正負號, 請問題目2的線性近似對於「增加功率」是低估還是高估呢? 那麼對於「減少阻力」呢? 利用你的答案解釋為什麼在功率或阻力的變化量不小的情況下, 「減少阻力」比較有效率?

問題 4:

畫出 $f(x, y)$ 的等高線圖, 解釋這些等高線的形狀和問題 2 和 3 有哪些關聯性.

解

畫出在 h= -0.75, -0.5, -0.25, 0, 0.05, 0.25, 0.5, 0.75, 1的等高線

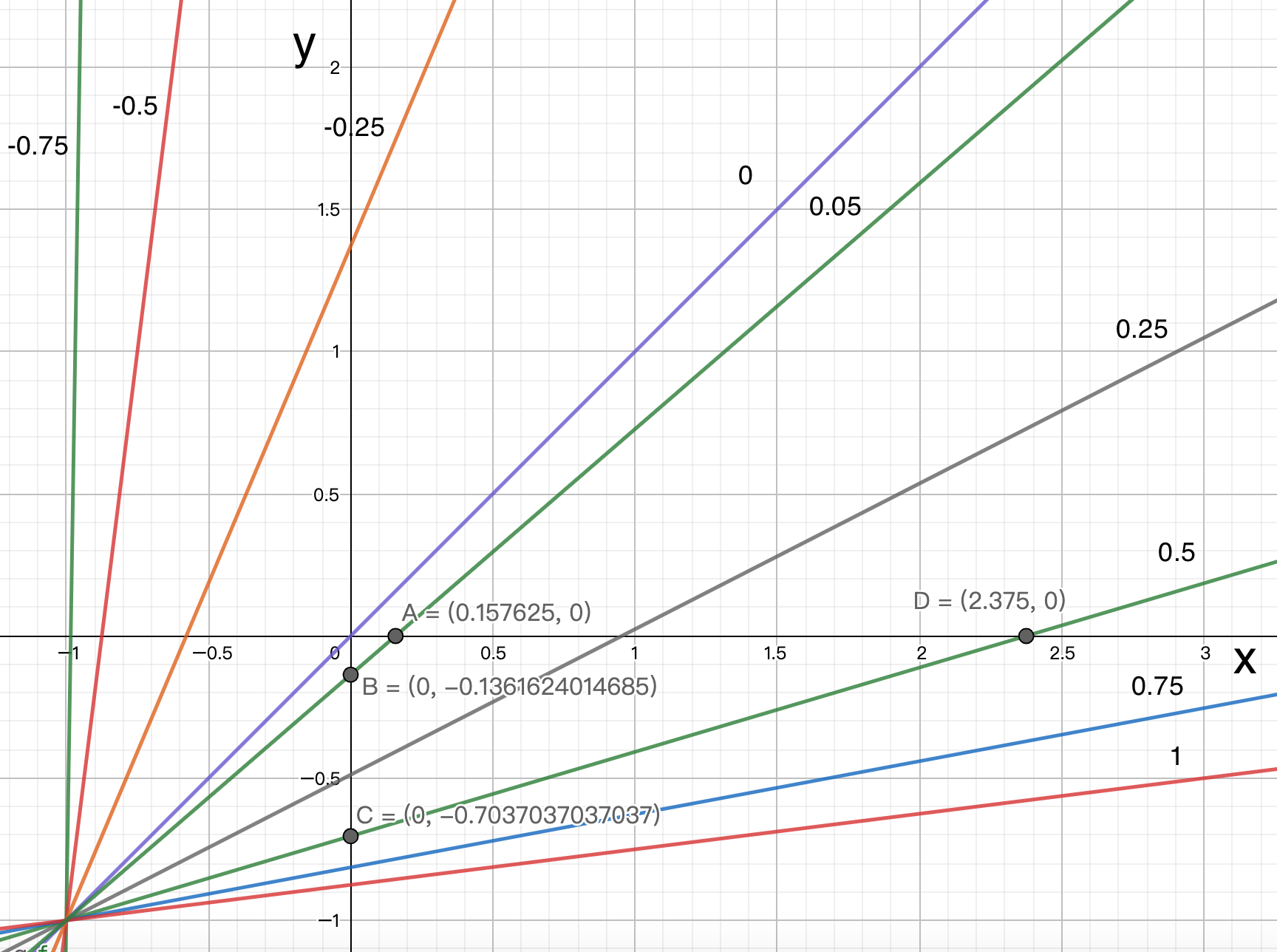
1. 當功率和阻力變化量很小

   假設在點 $(0, 0)$ 時很小的功率和阻力變化量導致 $h$ 從 $h=0$ 變化成 $h=0.05$. 為了從點 $(0,0)$ 達到 $h=0.05$, 功率需要增加大約 $0.158$ (點 A) 或者是阻力需要增加大概 $0.136$ (點 B), 這兩個值相當接近, 這個結果呼應了問題 2 的答案.

2. 當功率和阻力變化量較大

   假設在點 $(0, 0)$ 時較大的功率和阻力變化量導致 $h$ 從 $h=0$ 變化成 $h=0.5$. 為了從點 $(0, 0)$ 達到 $h=0.5$, 功率需要增加大約 $2.38$ (點 D) 或者是阻力需要增加大概 $0.704$ (點 C), 可見「減少阻力」比「增加功率」的效率還要高出約 $3.4$倍 ($2.38/0.74=3.4$), 這個結果呼應了問題 3 的答案.