Sec.12.4 - The Geometry of a Tetrahedron

Discovery Project in Sec.12.4, Calculus by Stewart
Chinese version 四面體的幾何學

A tetrahedron is a solid with four vertices, P ,Q , R and S ,and four triangular faces, as shown in the figure.

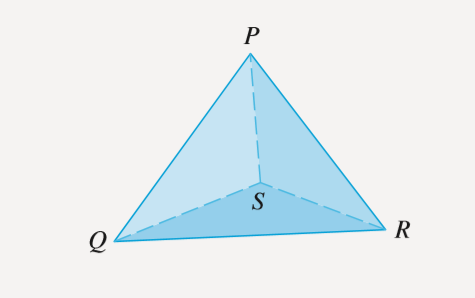
Question 1:

Let $v_1, v_2, v_3$ and $v_4$ be vectors with lengths equal to the areas of the faces opposite the vertices P, Q, R and S, respectively, and directions perpendicular to the respective faces and pointing outward. Show that $$ v_1+v_2+v_3+v_4=0 $$

Question 2:

The volume V of a tetrahedron is one-third the distance from a vertex to the opposite face, times the area of the face.

(a)Find a formula for the volume of a tetrahedron in terms of the coordination of its vertices P ,Q , R and S.

(b)Find the volume of the tetrahedron whose vertices are P(1,1,1), Q(1,2,3), R(1,1,2), and S(3,-1,2).

Answer:

(b)

By (a), a=(0,1,2), b=(0,0,1), c=(2,-2,1).

So $$ V=\frac{\left | \begin{array}{ccc} 0 & 1 & 2 \\
0 & 0 & 1 \\
2 & -2 & 1 \\
\end{array}\right |}{6}=\frac{1}{3} $$

Question 3:

Suppose the tetrahedron in the figure has a trirectangular vertex S. (This means that the three angles at S are all right angles.) Let A,B,and C be the areas of the three faces that meet at S,and let D be the area of the opposite face PQR. Using the result Question 1, or otherwise, show that $$ D^{2}=A^{2}+B^{2}+C^{2} $$ (This is a three-dimensional version of the Pythagorean Theorem.)