Sec.14.4 - The speedo LZR razer

Applied Project in Sec.14.4, Calculus by Stewart
Chinese version 速比濤鯊魚皮系列第四代泳裝

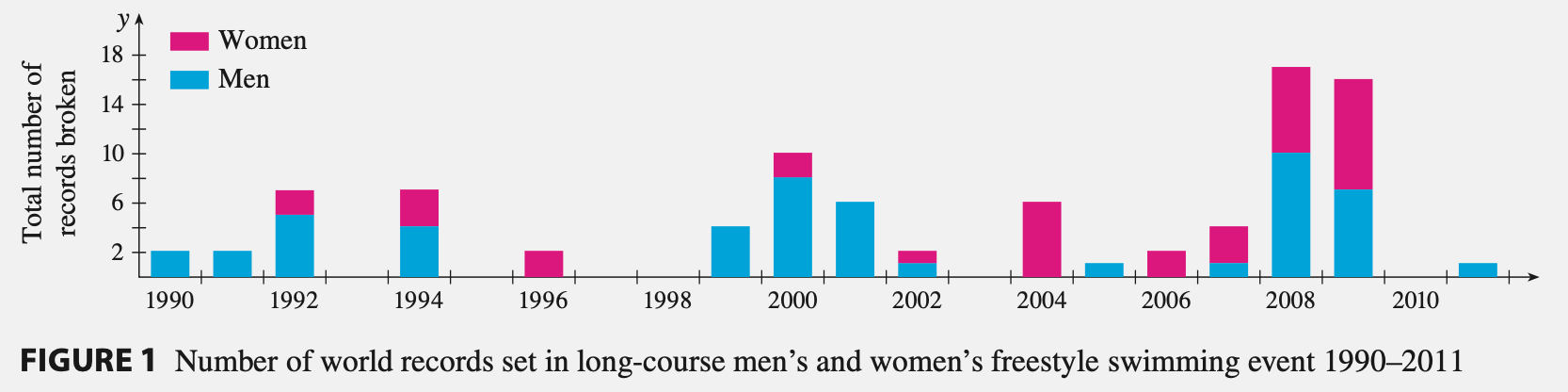
Many technological advances have occurred in sports that have contributed to increased athletic performance. One of the best known is the introduction, in 2008, of the Speedo LZR racer. It was claimed that this full-body swimsuit reduced a swimmer’s drag in the water. Figure 1 shows the number of world records broken in men’s and women’s long-course freestyle swimming events from 1990 to 2011. The dramatic increase in 2008 when the suit was introduced led people to claim that such suits are a form of technological doping. As a result all full-body suits were banned from competition starting in 2010.

It might be surprising that a simple reduction in drag could have such a big effect on performance. We can gain some insight into this using a simple mathematical model.

The speed $v$ of an object being propelled through water is given by $$ v(P,C)=\left(\frac{2P}{kC}\right)^{\frac{1}{3}}, $$ where $P$ is the power being used to propel the object, $C$ is the drag coefficient, and $k$ is a positive constant. Athletes can therefore increase their swimming speeds by increasing their power or reducing their drag coefficients. But how effective is each of these?

To compare the effect of increasing power versus reducing drag, we need to somehow compare the two in common units. The most common approach is to determine the percentage change in speed that results from a given percentage change in power and in drag.

If we work with percentages as fractions, then when power is changed by a fraction $x$ (with $x$ corresponding to $100x$ percent), $P$ changes from $P$ to $P + xP$. Likewise, if the drag coefficient is changed by a fraction $y$, this means that it has changed from $C$ to $C + yC$. Finally, the fractional change in speed resulting from both effects is $$ f(x,y)=\frac{v(P+xP,C+yC)-v(P,C)}{v(P,C)} $$

Question 1:

The function $f$ gives the fractional change in speed that results from a change $x$ in power and a change $y$ in drag. Show that this reduces to the function $$ f(x,y)=\left(\frac{1+x}{1+y}\right)^{\frac{1}{3}}-1. $$ Given the context, what is the domain of $f$?

Answer:

The domain of $f$ is $$ {(x,y)\mid x\geq-1,\quad y>-1} $$

Question 2:

Suppose that the possible changes in power $x$ and drag $y$ are small. Find the linear approximation to the function $f(x, y)$. What does this approximation tell you about the effect of a small increase in power versus a small decrease in drag?

Answer:

• The effect of a small increase in power vs. a small decrease in drag

  According to the linear approximation to the function $f$ , the small increase in power $x$ and the small decrease in drag $y$ have the same impact on changes in speed $f$ with the proportion of one-third. Consequently, in terms of the fractional change in speed, there is no significant difference between the small increase in power and the small decrease in drag.

Question 3:

Calculate $f_{xx}(x, y)$ and $f_{yy}(x, y)$. Based on the signs of these derivatives, does the linear approximation in Problem 2 result in an overestimate or an underestimate for an increase in power? What about for a decrease in drag? Use your answer to explain why, for changes in power or drag that are not very small, a decrease in drag is more effective.

Question 4:

Graph the level curves of $f(x, y)$. Explain how the shapes of these curves relate to your answers to Problems 2 and 3.

Answer:

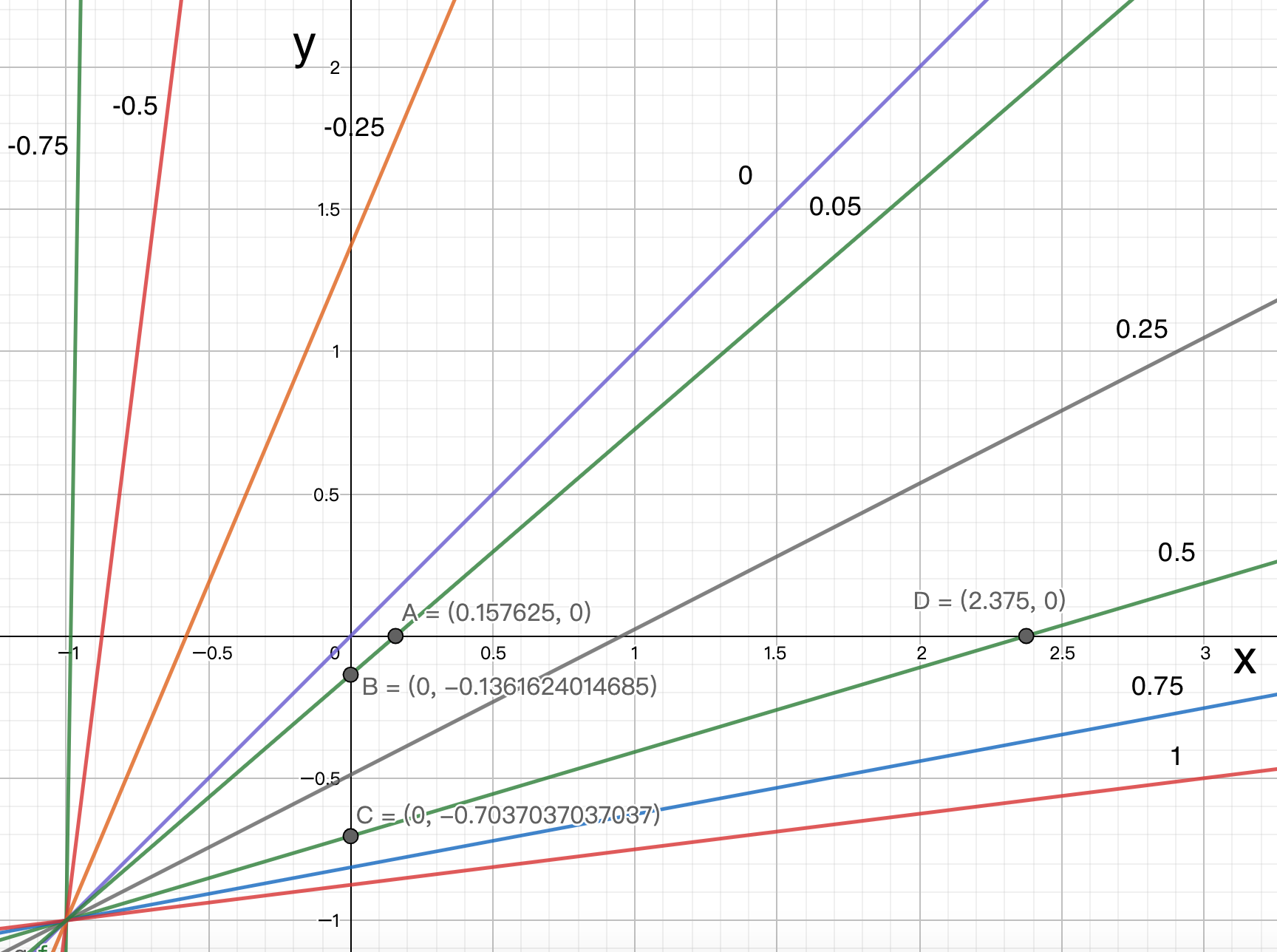
Graph the level curve with h= -0.75, -0.5, -0.25, 0, 0.05, 0.25, 0.5, 0.75, 1

1. A little changes in power or drags

   Suppose that a little changes in power or drags at point $(0, 0)$ leads to a change in $h$ from $h=0$ to $h=0.05$. In order to reach $h=0.05$ from point $(0, 0)$, the power has to increase about $0.158$ (point A), or the drag has to decrease about $0.136$ (point B). These two value are closed to each other. The result correspond with the answer of Problem 2.

2. A considerable changes in power or drags

   Suppose that a considerable changes in power or drags at point $(0, 0)$ leads to a change in $h$ from $h=0$ to $h=0.5$. In order to reach $h=0.5$ from point $(0, 0)$, the power has to increase about $2.38$ (point D), or the drag has to decrease $0.704$ (point C). The decrease in drag is about 3.4 times more efficient than the increase in power. $(2.38/0.74=3.4)$ The result correspond with the answer of Problem 3.