Sec.12.4 - 四面體的幾何學

Discovery Project in Sec.12.4, Calculus by Stewart
英文版請見 The Geometry of a Tetrahedron

如圖所示，四面體是一個擁有4個頂點(P,Q,R,S)和四個三角面的固體。

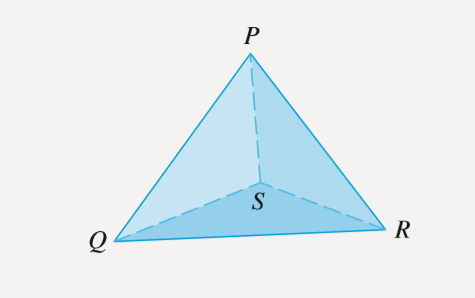
問題1：

令 $v_1, v_2, v_3$ 和 $v_4$ 為向量, 其長度分別和頂點 P$, $Q$, $R$, $S 所對應到的面的面積相等，並且其方向與對應到的面垂直且向外。證明 $$ v_1+v_2+v_3+v_4=0 $$

問題2：

四面體的體積V是其一頂點到其對面的距離乘以該面的面積，再乘以三分之一倍。

(a)找出一個計算四面體體積的公式，以頂點 P，Q，R，S 的座標表達。

(b)算出四頂點分別為 P(1,1,1)，Q(1,2,3)，R(1,1,2)，S(3,-1,2) 的四面體的體積。

解答:

(b)

由 (a), a=(0,1,2), b=(0,0,1), c=(2,-2,1).

所以 $$ V=\frac{\left | \begin{array}{ccc} 0 & 1 & 2 \\
0 & 0 & 1 \\
2 & -2 & 1 \\
\end{array}\right |}{6}=\frac{1}{3} $$

問題3:

假設如圖所示的四面體有一個三直角的頂點S。(這表示三個在S的角是直角。) 令A，B，C為三個在S相遇的面，且令D為相對的面PQR。用問題1的結論，或其他方法證明 $$ D^{2}=A^{2}+B^{2}+C^{2} $$ (這是一個三維版本的勾股定理。)