Sec.11.11 - 恆星的輻射

Applied Project in Sec.11.11, Calculus by Stewart
英文版請見 Radiation From The Stars

任何物件在被加熱時會散發輻射. 而 黑體 則是一個會吸收所有經過他的輻射的一個系統. 舉例來說, 一個表面黑色且沒有光澤或著有一個大的空腔但只有一個小孔洞在牆壁上(像是煉鐵的高爐)可以視為一個黑體, 而他們會散發黑體輻射. 甚至從太陽散發出來的輻射也可以視作為一種黑體輻射.

19世紀時, 瑞立-金斯定律(Rayleigh-Jeans Law)被提出來, 用來描述黑體輻射的能量密度和波長 $\lambda$ 的關系: $$ f(\lambda)=\frac{8 \pi kT}{\lambda^4} $$ 其中 $\lambda$ 的單位是公尺, $T$ 是溫度單位是 $K$(克氏溫標), $k$ 是波茲曼常數(Boltzmann’s constant) $= 1.3807\times 10^{-34} (J/K)$.

瑞立-金斯定律與實驗測量結果相比, 在長波長是吻合的, 但在短波長時卻相差甚遠. (這個定理預測 $f(\lambda)\rightarrow \infty$ as $\lambda \to 0^+$ 但實驗結果卻顯示 $f(\lambda)\to 0$.) 這個結果後來被稱為 紫外災變.

馬克思.普朗克 (Max Planck) 在 1990 時為黑體輻射找到一個更好的模型(現在被稱為普朗克定律): $$ f(\lambda)= \frac{8 \pi hc \lambda^{-5}}{e^{hc/(\lambda kT)}-1} $$ 其中

• $h$ 是普朗克常數(Plancks’s constant) = $6.626\times 10^{-34} (J\cdot s)$
• $c$ 是光速 $= 2.997925\times 10^8 (m/s)$

Question 1：

用羅畢達法則 (l’Hospital’s Rule) 說明普朗克定律

$$ \lim_{\lambda\to 0^+}f(\lambda) = 0 $$ and $$ \lim_{\lambda\to\infty} f(\lambda) = 0 $$ 此結果說明為何對短波長的黑體輻射普朗克的模型比瑞立-金斯的定理更好.

Question 2：

用泰勒展開式(Taylor polynomial) 說明在長波長時,普朗克定律 和 瑞立-金斯定理的結果會大致相同.

Question 3：

分別用兩個函式在同一個座標平面上劃出圖形, 並且說明相同和相異之處. $T$ 用 5700K (太陽表面溫度) 帶入. (為了更方便計算 可以把長度單位從公尺換成微米: $1\mu$m = $10^{-6}$ m.)

Answer:

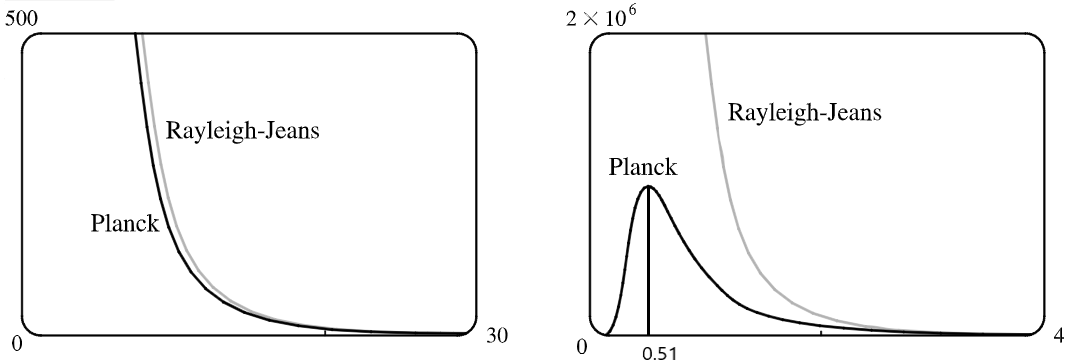
為了轉換成微米,我們把 $\lambda$ 用 $\frac{\lambda}{10^6}$ 帶入兩個函式. 在 $\lambda$ 很大時(圖左),兩個定理的結果很類似,然而在 $\lambda$ 很小時(圖右),結果差異甚大.

Question 4：

用第三題畫出來的圖去估算普朗克定律中 $f(\lambda)$ 為最大值時 $\lambda$ 的長度.

Answer:

從第三題的圖表得知, 普朗克定律中$f(\lambda)$ 在 $\lambda$ $\approx$ $0.51\mu$m 有最大值.

Question 5：

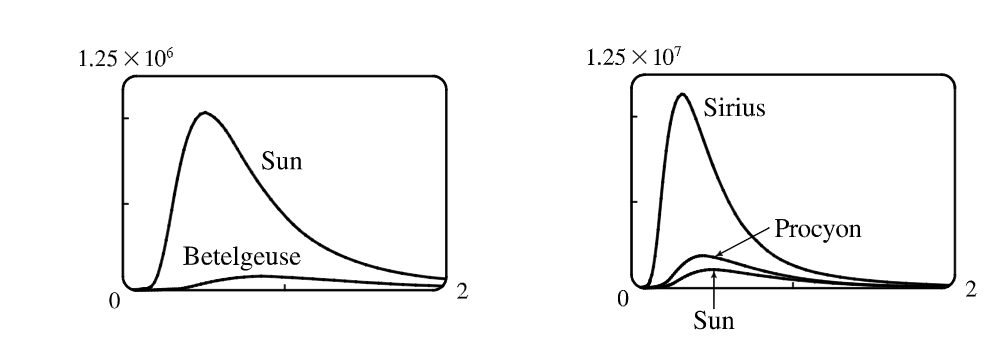
觀察下列四個恆星在普朗克定律的圖形 $f$ 如何隨著 $T$ 的變動

• 參宿四 (Betelgeuse) T = 3400K
• 南河三 (Procyon) T = 6400K
• 天狼星 (Sirius) T = 9200K
• 太陽

發散的總輻射量(曲線下的面積)式怎麼隨著溫度變化的? 用圖來說明為何天狼星是藍色而參宿四是紅色.

Answer:

隨著溫度升高，曲線下的面積也隨之增加，所以可以推斷出當恆星溫度越高，發散的能量越多。且當溫度升高時，曲線最大值的$\lambda$值會減少。因此溫度越高，恆星散發的光的峰值與平均波長越短。當光的波長越短，頻率越高。當頻率高時，光在光譜上會接近藍端。而參宿四的頻率較低，較接近紅端。這就是為什麼天狼星是藍星而參宿是紅星。