Polar curve - Example

這裡我們要介紹 $r^2=\cos(4\theta)$ 這個方程式的圖形怎麼畫.

首先, 因為 $r^2 \ge 0$, 所以整個方程式只有在 $\cos 4\theta \ge 0$ 的地方有定義.

我們先找離 $\theta=0$ 最近的一段定義域, 也就是 $$ -\frac{\pi}{8}\le \theta \le \frac{\pi}{8}. $$ 在這範圍內 $\cos(4\theta)\ge 0$ 所以沒問題.

接著我們試著把方程式寫成函數的樣子, 改寫成 $r = \pm\sqrt{\cos(4\theta)}$. 當然這樣不是函數, 所以應該是寫成兩個函數 $$ r = \sqrt{\cos(4\theta)}, \quad -\frac{\pi}{8}\le \theta \le \frac{\pi}{8}, $$ 以及 $$ r = -\sqrt{\cos(4\theta)}, \quad -\frac{\pi}{8}\le \theta \le \frac{\pi}{8}. $$

接著把這兩個函數分別畫出來就會得到兩片葉子.

接著我們找另一段有定義地方: $$ \frac{3\pi}{8}\le \theta \le \frac{5\pi}{8}. $$ 照以上一模一樣的步驟可以得到兩個函數 $$ r = \sqrt{\cos(4\theta)}, \quad \frac{3\pi}{8}\le \theta \le \frac{5\pi}{8}, $$ 以及 $$ r = -\sqrt{\cos(4\theta)}, \quad \frac{3\pi}{8}\le \theta \le \frac{5\pi}{8}. $$

把這兩個函數分別畫出來就會得到另外兩片葉子.

• 想要驗證自己畫得對不對可以對照以下圖形

  

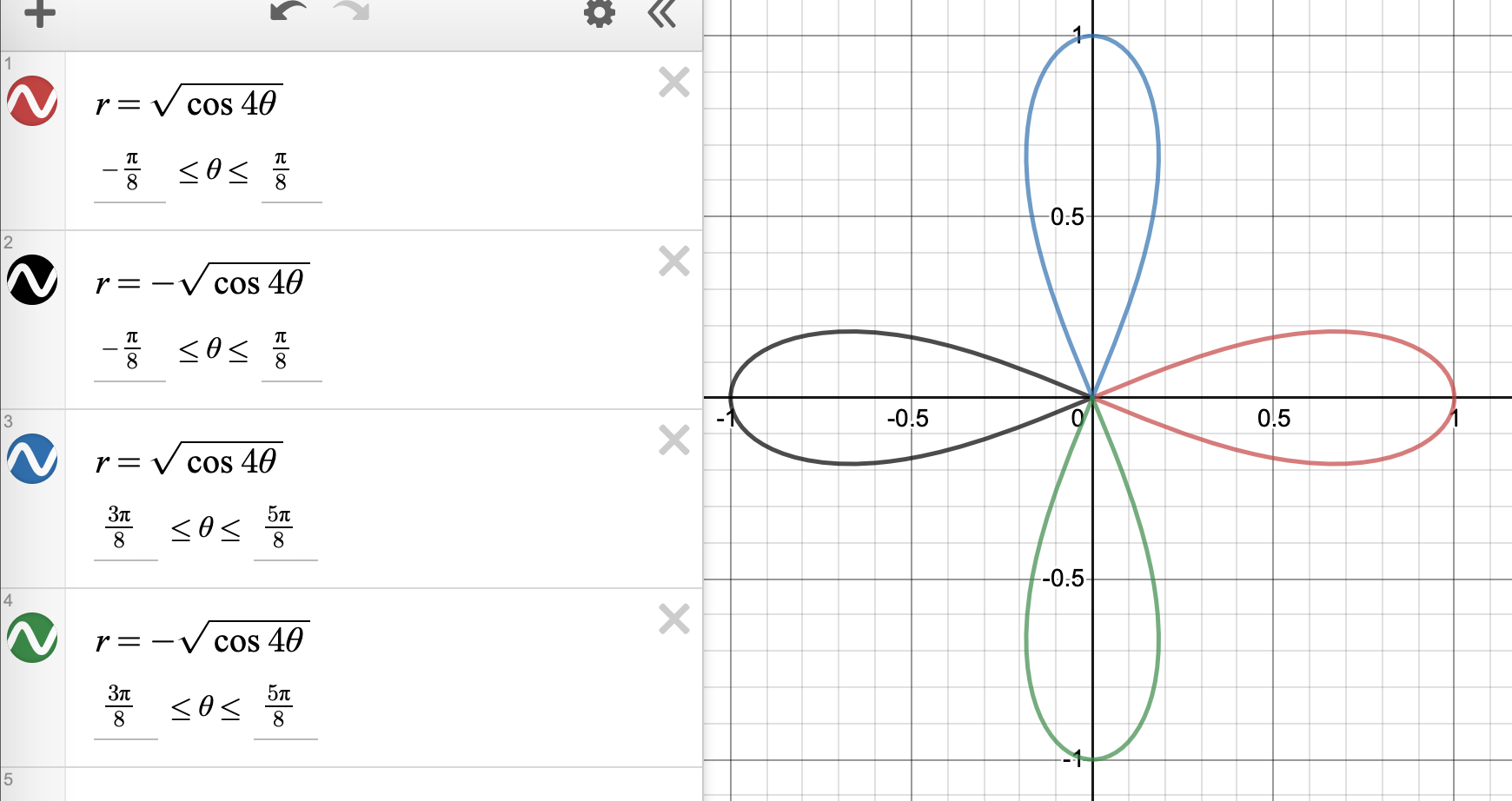
• 這個圖形我有點偷懶是用線上做圖畫的 polar curve on-line

當然, $\cos(4\theta) \ge 0$ 的定義域還有更多區間. 不過再多找一兩個區間會發現, 做出來的圖與以上四片葉子重複了. 所以整個函數圖形就是這四片葉子.