Sec.3.1 - 建造較佳的雲霄飛車

Applied Project in Sec.3.1, Calculus by Stewart
英文版請見 Building a better roller coaster

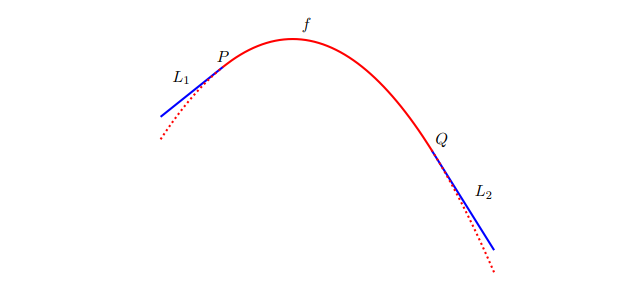
假設你被要求設計一架新的雲霄飛車的第一個上升與下降。在研究你最喜歡的雲霄飛車的圖片後，你決定新的雲霄飛車先以 0.8 的斜率上升然後再以 -1.6 的斜率下降。你決定以二次曲線 $y=f(x)=ax^2+bx+c$ 的一部份去連接上升與下降的直線 $y=L_1(x)$、$y=L_2(x)$，$x$和$f(x)$的單位為公尺。為了維持軌道的平滑性，因此軌道的方向上不能有明顯的變化，所以你要求兩條直線 $L_1$ 和 $L_2$ 應在交接點 $P$ 和 $Q$ 與二次曲線 $y=f(x)$ 相切（如圖）。你將起點定在 $P$ 以簡化方程式。

問題 1:

(a) 假設 $P$ 和 $Q$ 之間的水平距離是 30 公尺。請寫出以$a$、$b$、和$c$構成的等式使得軌道與軌道之間的接點是平滑的。

(b) 解出第(a)小題的 $a$、$b$、和 $c$，以找到$f(x)$的方程式。

(c) 畫出$L_1$、$f$和 $L_2$，以圖形證實軌道之間的接點是平滑的。

(d) 找出$P$和$Q$之間的垂直距離。

解答:

下圖是這些函數的圖形：

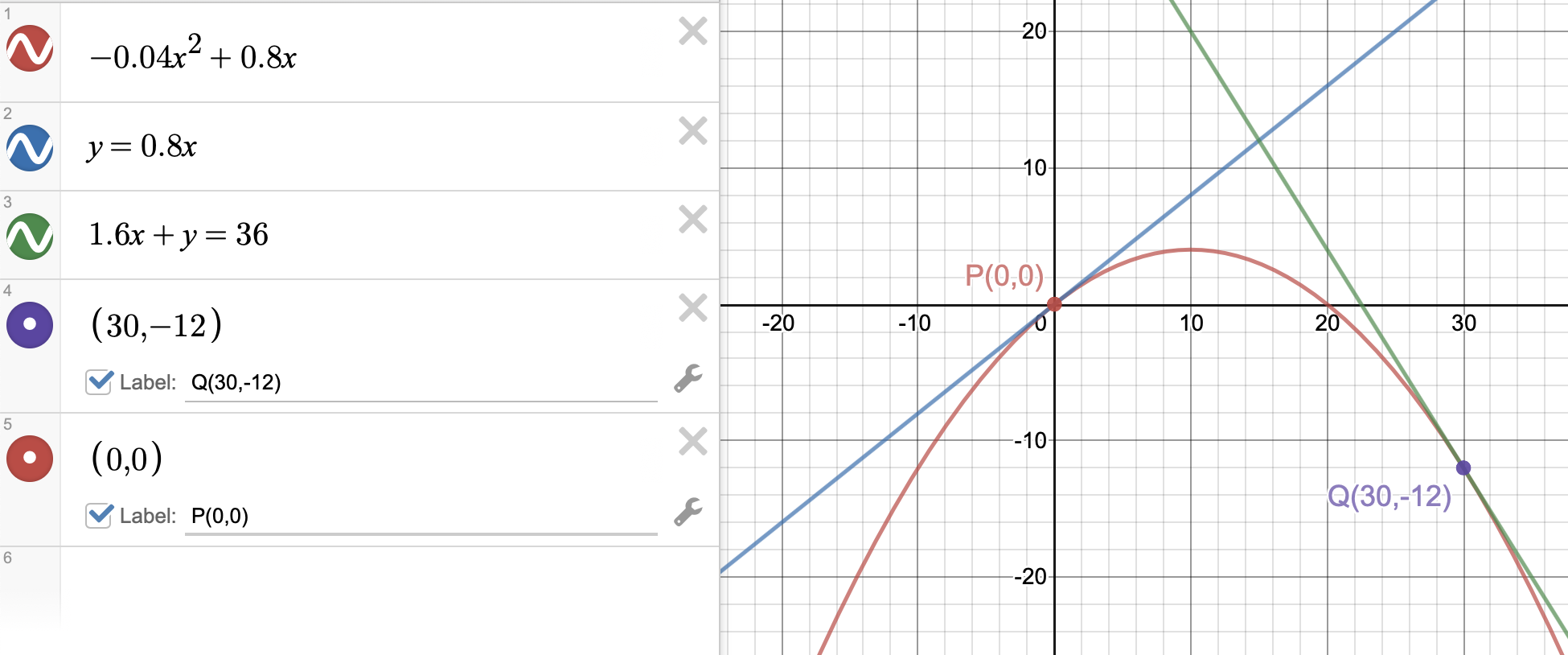
如上圖，$L_1$、$f$和$L_2$之間的接點是平滑的。

問題 2:

問題一的解答看似平滑，但坐起來感覺卻不怎麼平滑，因為分段定義的函數（$L_1(x)$ 當 $x<0$，$f(x)$ 當 $0\leq x\leq 30$，$L_2(x)$ 當 $x>30$）的二次微分並不連續。所以你決定將二次曲線 $q(x)=ax^2+bx+c$ 的使用範圍減少為 $3\leq x\leq 27$，並且將二次曲線和直線以兩條三次曲線相連接:

$$ g(x)=kx^3+lx^2+mx+n \quad 0 \leq x<3 $$

$$ h(x)=px^3+qx^2+rx+s \quad 27<x\leq 30 $$

(a) 列出含有11個未知數的一系列的方程式，使得接點與接點之間的一次微分及二次微分皆是相同的。

(b) 利用電腦計算系統解出第(a)小題的等式，以找出$q(x)$、$g(x)$和$h(x)$的方程式。

(c) 畫出 $L_1$、 $g$、 $q$、 $h$和 $L_2$，並與問題一的第(c)小題的圖形相互比較。

解答:

以下為更加平滑的軌道的圖形：