Sec.14.7 - 設計垃圾桶

Applied Project in Sec.14.7, Calculus by Stewart
English version Designing a dumpster

在這個專題中，我們先測量出一個長方體垃圾桶出他的外型和結構。希望設計出一個和它一樣大的容器，並將所需的花費最小化。

問題 1 :

首先，測量垃圾桶的大小，形狀和體積，並畫出垃圾桶的圖案。

答案：

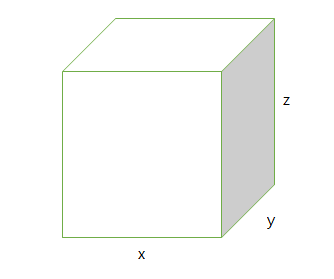
• 長 $x = 0.2 (m)$
• 寬 $y = 0.25 (m)$
• 高 $z = 0.3 (m)$

$$ 體積 = 0.2 \times 0.25 \times 0.3 = 0.015 (m^3) $$

問題 2：

維持垃圾桶大概的形狀，設計出一個體積和原垃圾桶相同而且價格最便宜的容器。使用下列條件進行分析:

• 前後和側邊都是用12-gauge (厚度 $2.657$ 毫米) 的鋼板做成，價格為每平方公尺$8.00
• 底部是由10-gauge (厚度 $3.416$ 毫米) 的鋼板製成，價格為每平方公尺 $10.00
• 蓋子不論大小，每片約 $50.00
• 焊接的價格為每公尺 $0.60

自行提出其他假設，敘述所設計的容器

答案：

從上面的規定，我們可以算出長方體容器價格的方程式: $$ 8\times 2\times (x+y)\times z+10xy+50+0.6\times (2x+2y+4z) $$ 其中x是寬，y是長，z是高 ，容器的體積和垃圾桶一樣，為$0.015 m^3$ ，因此我們可以得到： $$ xyz=0.015\ or\ z=\frac{0.015}{xy} $$ 所以可以將花費的式子 $f$ 改寫成： $$ f=0.24\left(\frac{1}{x}+\frac{1}{y}\right)+10xy+50+1.2x+1.2y+\frac{0.036}{xy} $$ 如果$f$要是最小值，那 $f_x=f_y=0$, 其中 $$ f_x=\frac{-0.24}{x^2}+10y+1.2-\frac{0.036}{x^2y}\
f_y=\frac{-0.24}{y^2}+10x+1.2-\frac{0.036}{xy^2} $$ 但是x 和y 一定是正數，所以 x=y。接著，將x=y 帶入偏微分的式子，可以得到 $10x^4+ 1.2x^3 -0.24x -0.036=0$，能夠找出長方體容器的長寬高： $$ x=寬=y=長\approx0.295\
z=高\approx0.172\
$$ 總花費=TotalCost=$53.61473

問題 3:

描述所做的假設或省略會帶來怎麼樣的影響

答案 :

因為容器的長寬高和容器壁的厚度大小差距約100倍，因此我將厚度忽略。

問題 4：

如果我變成這個研究的顧問，我的結論會是？我會建議更換垃圾桶的設計嗎？如果會的話，能夠省下多少錢？

答案：

原本垃圾桶的花費要 $53.92，比我們設計的容器還要貴，因此如果只從成本方面考量，我會建議更改垃圾桶的設計，可以省下至少$0.3。