Sec.14.7 - Designing a dumpster
Applied Project in Sec.14.7, Calculus by Stewart
Chinese version 設計垃圾桶
For this project we locate a rectangular trash Dumpster in order to study and describe all its shape and construction. We then attempt to determine the dimensions of a container of similar design that minimize construction cost.
Question 1 :
First locate a trash dumpster in your area. Carefully study and describe all details of its construction, and determine its volume. Include a sketch of the container.
Answer:
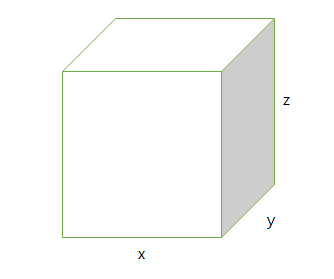
- Width $x = 0.2 (m)$
- Length $y = 0.25 (m)$
- Height $z = 0.3 (m)$
$$ volume = 0.2 \times 0.25 \times 0.3 = 0.015 (m^3) $$
Question 2:
While maintaining the general shape and method of construction, determine the dimensions such a container of the same volume should have in order to minimize the cost of construction. Use the following assumptions in your analysis:
- The sides, back, and front are to be made from 12-gauge ($2.657 (mm)$ thick) steel sheets, which cost $8.00 per square foot (including any required cuts or bends).
- The base is to be made from a 10-gauge ($3.416 (mm)$ thick) steel sheet, which costs $10.00 per square foot.
- Lids cost approximately $50.00 each, regardless of dimensions.
- Welding costs approximately $0.60 per square meter for material and labor combined.
Give justification of any further assumptions or simplifications made of the details of construction.
Answer:
From these figures the cost equation of a rectangular dumpster was determined to be:
$$
8\times 2\times (x+y)\times z+10xy+50+0.6\times (2x+2y+4z)
$$
Where the dimensions are based on a 3-dimentional graph, Width=x, Length=y, and Height=z. It is also known that the dumpster volume will have to equal to $0.015 (m^3)$, i.e.,
$$
xyz=0.015\ or\ z=\frac{0.015}{xy}
$$
so the expression for Total Cost $(f)$ becomes
$$
f=0.24\left(\frac{1}{x}+\frac{1}{y}\right)+10xy+50+1.2x+1.2y+\frac{0.036}{xy}
$$
To have a minimum we should have $f_x=f_y=0$ where
$$
f_x=\frac{-0.24}{x^2}+10y+1.2-\frac{0.036}{x^2y}\
f_y=\frac{-0.24}{y^2}+10x+1.2-\frac{0.036}{xy^2}
$$
Since $x$ and $y$ must be positive in this problem, we have $x=y$. We then get $10x^4+ 1.2x^3 -0.24x -0.036=0$ that has only one positive root $x\approx 0.295$.
So we find Total cost is about $53.6.
Question 3:
Describe how any of your assumptions or simplifications may affect the actual result.
Answer:
Since the length of the side is much bigger then it’s thickness we simply ignore the thickness.
Question 4:
If you were hired as a consultant on this investigation, what would your conclusion be? Would you recommend altering the design of the dumpster? If so, describe the savings that would result.
Answer
The cost of the original trash dumpster is $53.92, which is larger than the dumpster we design. So we would recommend altering the design of the dumpster, and we can save about $0.3.