Sec.10.3 - 極座標曲線家族

Laboratory Project in Sec.10.3, Calculus by Stewart English version: Families of Polar Curves

在這個研究中，你將發現極座標曲線家族有趣又漂亮的形狀。同時，當常數改變時，你也會觀察到曲線形狀的變化。

問題 1:

(a) 探討以下列極座標方程式： $r=\sin(n\theta)$ 定義的曲線家族，其中 $n$ 為正整數。請問圖形中的環的數量與 $n$ 有何關係？

(b) 若將 (a) 中方程式改成 $r= |\sin(n\theta)|$ ，會發生什麼事？

解答:

(a)

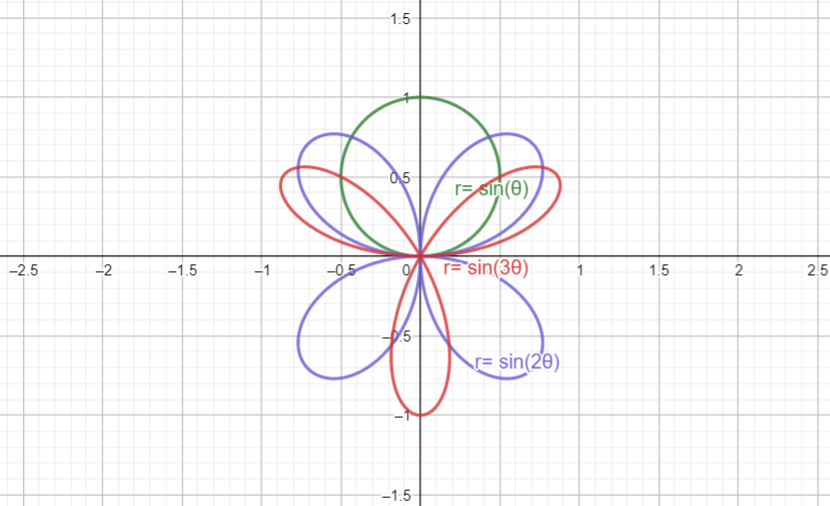
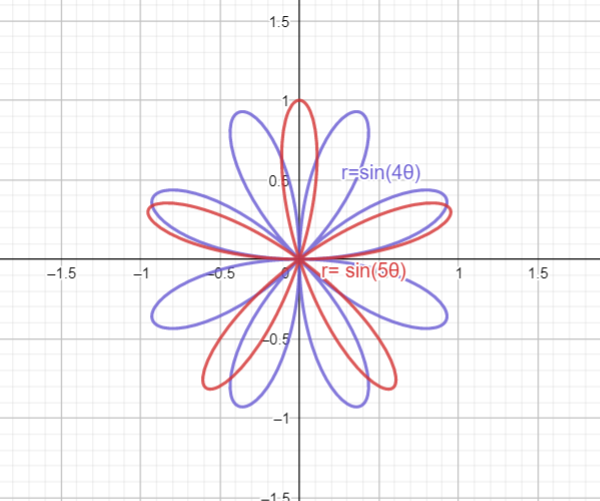
我們發現當 $n$ 為奇數, 環的數量為$n$, 而當 $n$ 為偶數, 環的數量為$2n$.

(b)

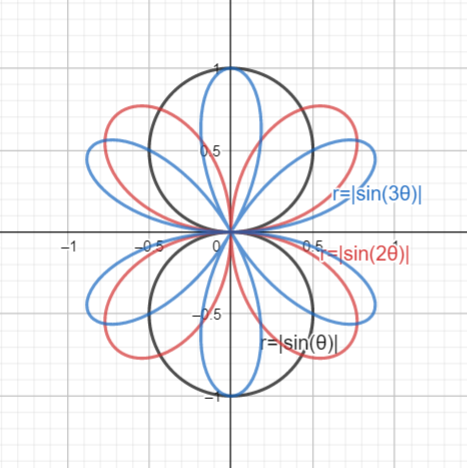
我們發現環的數量恆為$2n$ 。

問題 2:

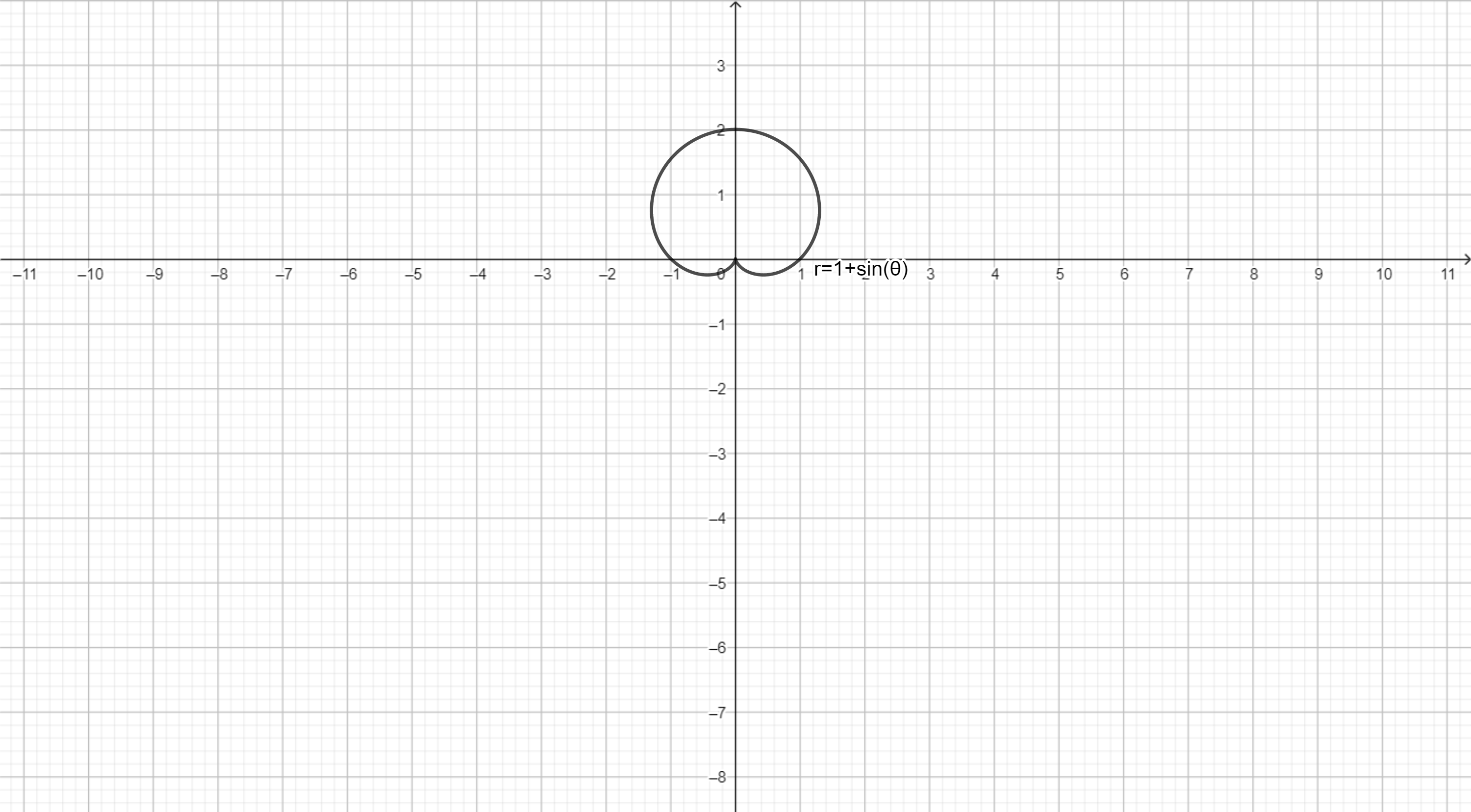
有一曲線家族由方程式 $r=1+c\sin(n\theta)$ 定義，其中 $c$ 為實數，$n$ 為正整數。請問隨 $n$ 值增加，曲線圖形會如何改變？隨 $c$ 值改變，圖形又會如何改變？繪出此曲線家族中足夠的成員來說明，以支持你的結論。

解答:

• $c=1$, $n=1$

  

• $c=1$, $n=2$

  

• $c=1$, $n=3$

  

  • 隨 $n$ 值增加，環數增加，環數等於 $n$，當 $|c|>1$，則環數等於 $2n$。

  • $c$ 值的絕對值增加，使圖形多出 $n$ 個小環後，小環和大環會漸漸變大。

• $n=1$

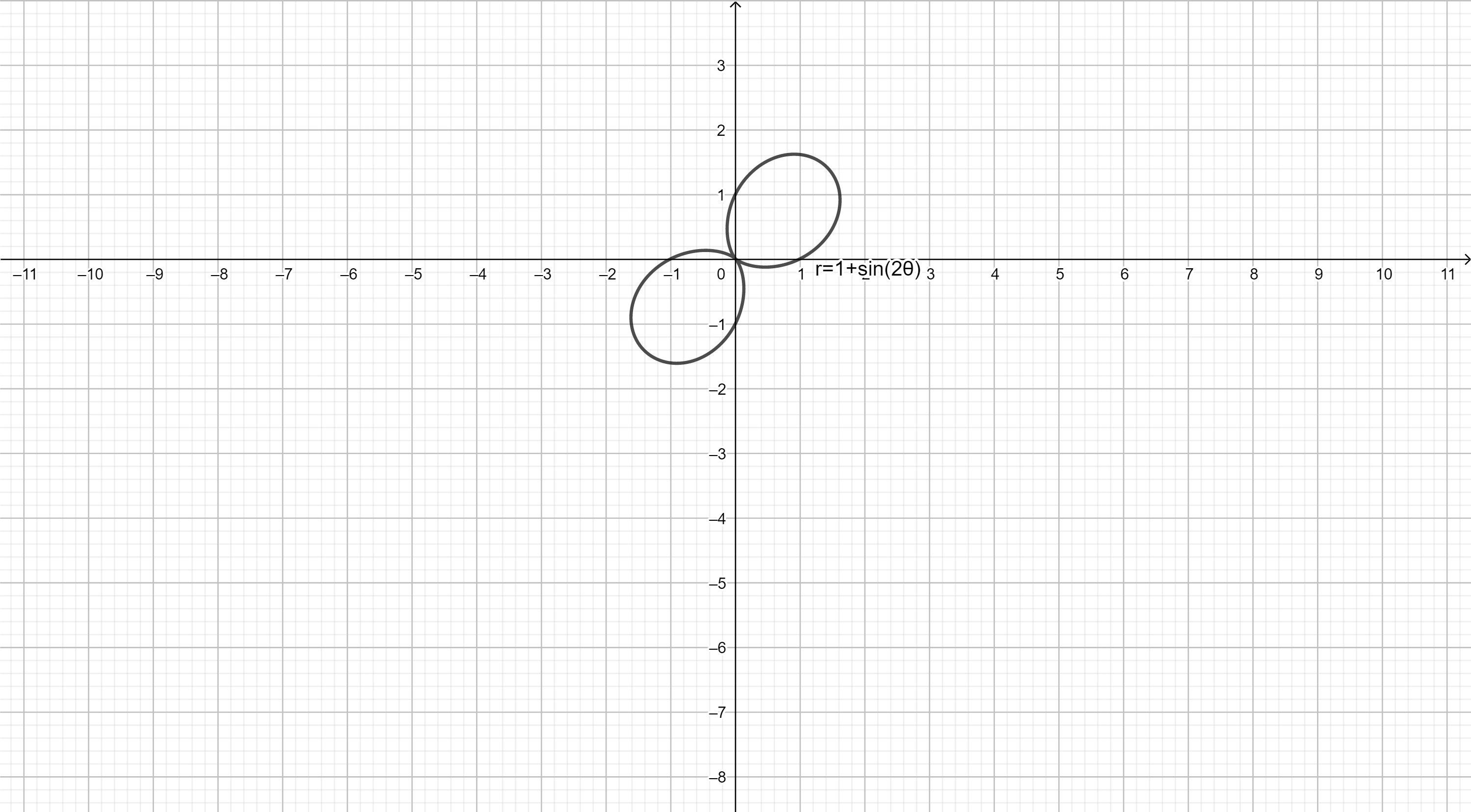
• $n=2$

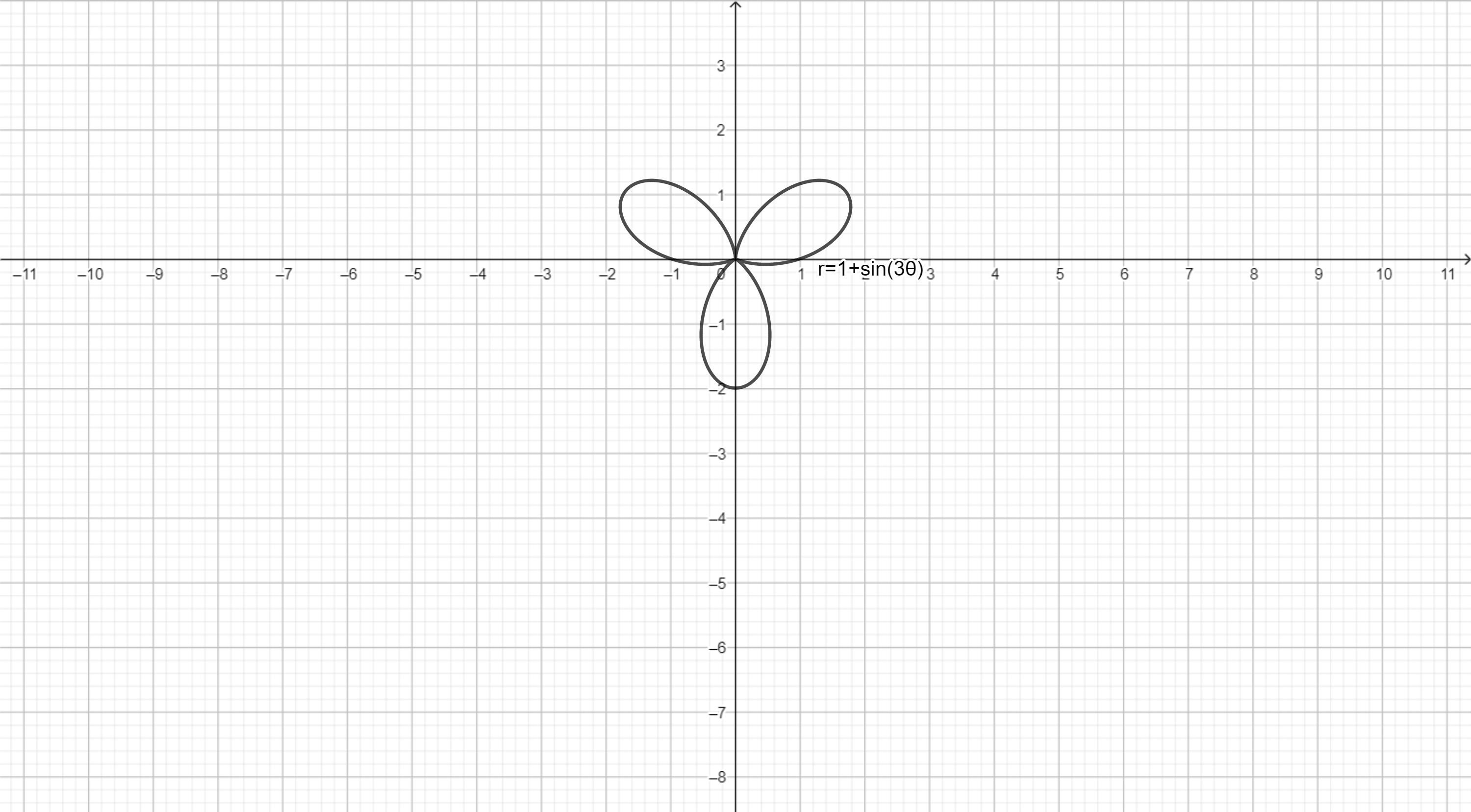
• $n=3$

問題 3:

有一曲線家族有極座標方程式 $r= \frac{1-acos\theta}{1+acos\theta}$, 探討隨$a$ 值改變，圖形會如何改變。你應該特別辨別曲線基本形狀改變時的$a$ 值。

解答:

隨著 $a$ 絕對值增加，圓形逐漸變桃型，當$|a|>1$ ，桃型尖端向內形成另一小環。隨 $a$ 值增加，小環逐漸變大。

問題 4:

天文學家喬凡尼·多美尼科·卡西尼 (1625-1712) 研究有極座標方程式 $r^4 -2c^2r^2\cos(2\theta)+c^4-a^4=0$ 的曲線家族，其中 $a$ 和 $c$ 為正實數。這些曲線叫做卡西尼卵形線，即便它們只有在特定 $a$ 值和 $c$ 值才會呈卵形。（卡西尼認為這些曲線，比起克卜勒的橢圓，可能更能代表行星軌道。）探討這些曲線的各種形狀。尤其，當曲線裂成兩部分時，$a$ 和 $c$ 彼此關係為何？

解答:

• $a=1$

• $c=1$

卡西尼卵形線主要有三種形狀，倒8形狀、包含兩焦點的環以及各包含一焦點的兩環。當環曲線裂成兩部分時，代表在極座標中的某些$\theta$ 值，$r$ 不存在。

令 $A=r^2$, 方程式可以改寫成 $A^2- 2c^2A \cos(\theta) +c^4 -a^4 =0$. 此二次方程式的判別式為 $$ D = 4c^4 cos^2(2\theta) -4(c^4 -a^4) = 4\left(a^2-c^2\sin^2(2\theta)\right) $$ 當 $|a|<|c|$，將存在某些$\theta$ 值， $D<0$, 則 $A$ 無實數解因此 $r$ 不存在。