A shallow physics-informed neural network for solving partial differential equations on surfaces

Abstract

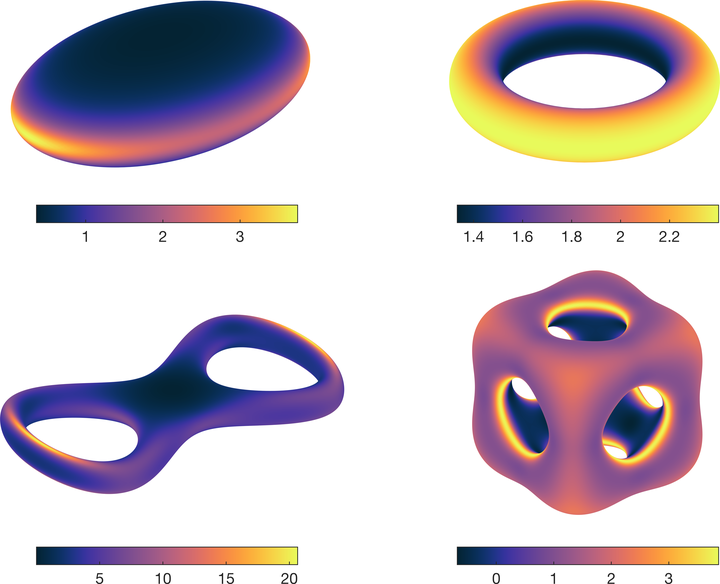
In this paper, we introduce a mesh-free physics-informed neural network for solving partial differential equations on surfaces. Based on the idea of embedding techniques, we write the underlying surface differential equations using conventional Cartesian differential operators. With the aid of level set function, the surface geometrical quantities, such as the normal and mean curvature of the surface, can be computed directly and used in our surface differential expressions. So instead of imposing the normal extension constraints used in literature, we take the whole Cartesian differential expressions into account in our loss function. Meanwhile, we adopt a completely shallow (one hidden layer) network so the present model is easy to implement and train. We perform a series of numerical experiments on both stationary and time-dependent partial differential equations on complicated surface geometries. The result shows that, with just a few hundred trainable parameters, our network model is able to achieve high predictive accuracy.