Abstract
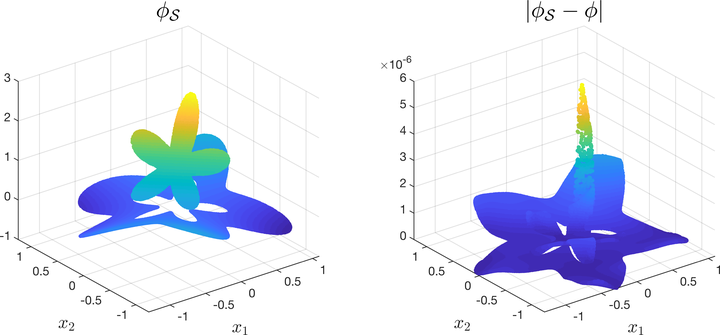
In this paper, a new Discontinuity Capturing Shallow Neural Network (DCSNN) for approximating $d$-dimensional piecewise continuous functions and for solving elliptic interface problems is developed. There are three novel features in the present network; namely, (i) jump discontinuity is captured sharply, (ii) it is completely shallow consisting of only one hidden layer, (iii) it is completely mesh-free for solving partial differential equations (PDEs). We first continuously extend the $d$-dimensional piecewise continuous function in $(d+1)$-dimensional space by augmenting one coordinate variable to label the pieces of discontinuous function, and then construct a shallow neural network to express this new augmented function. Since only one hidden layer is employed, the number of training parameters (weights and biases) scales linearly with the dimension and the neurons used in the hidden layer. For solving elliptic interface equations, the network is trained by minimizing the mean squared error loss that consists of the residual of governing equation, boundary condition, and the interface jump conditions. We perform a series of numerical tests to compare the accuracy and efficiency of the present network. Our DCSNN model is comparably efficient due to only moderate number of parameters needed to be trained (a few hundreds of parameters used throughout all numerical examples here), and the result shows better accuracy (and less parameters) than other method using piecewise deep neural network in literature. We also compare the results obtained by the traditional grid-based immersed interface method (IIM) which is designed particularly for elliptic interface problems. Again, the present results show better accuracy than the ones obtained by IIM. We conclude by solving a six-dimensional problem to show the capability of the present network for high-dimensional applications.