Abstract
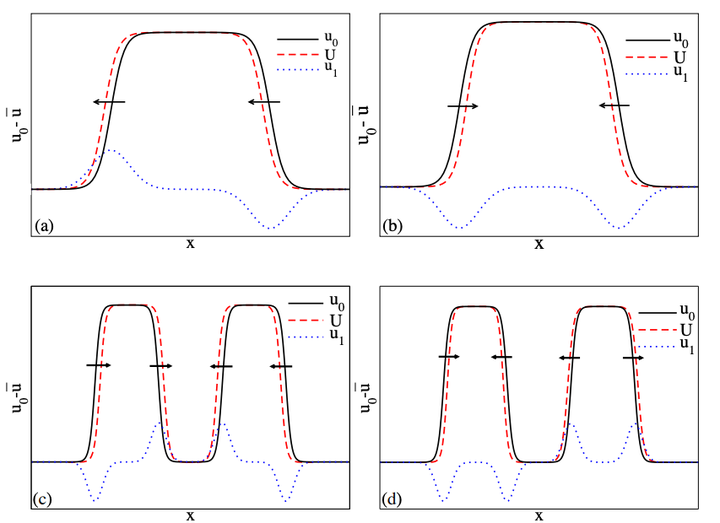
We consider the Cahn-Hilliard (CH) equation with a Burgers-type convective term that is used as a model of coarsening dynamics in laterally driven phase-separating systems. In the absence of driving, it is known that solutions to the standard CH equation are characterized by an initial stage of phase separation into regions of one phase surrounded by the other phase (i.e., clusters or drops/holes or islands are obtained) followed by the coarsening process, where the average size of the structures grows in time and their number decreases. Moreover, two main coarsening modes have been identified in the literature, namely, coarsening due to volume transfer and due to translation. In the opposite limit of strong driving, the well-known Kuramoto-Sivashinsky (KS) equation is recovered, which may produce complicated chaotic spatio-temporal oscillations. The primary aim of the present work is to perform a detailed and systematic investigation of the transitions in the solutions of the convective CH (cCH) equation for a wide range of parameter values, and, in particular, to understand in detail how the coarsening dynamics is affected by an increase of the strength of the lateral driving force. Considering symmetric two-drop states, we find that one of the coarsening modes is stabilized at relatively weak driving, and the type of the remaining mode may change as driving increases. Furthermore, there exist intervals in the driving strength where coarsening is completely stabilized. In the intervals where the symmetric two-drop states are unstable they can evolve, for example, into one-drop states, two-drop states of broken symmetry or even time-periodic two-drop states that consist of two traveling drops that periodically exchange mass. We present detailed stability diagrams for symmetric two-drop states in various parameter planes and corroborate our findings by selected time simulations.