A direct Poisson solver in spherical geometry with an application to diffusiophoretic problems

Abstract

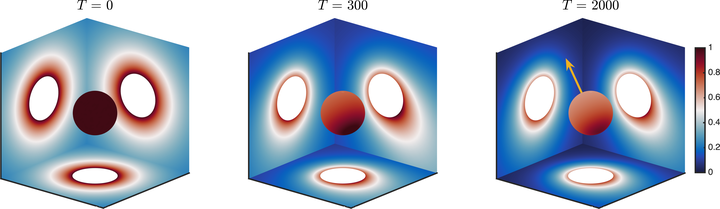
We propose a simple and efficient class of direct solvers for Poisson equation in finite or infinite domains related to spherical geometry. The solver was developed based on truncated spherical harmonics expansion, where the differential mode equations were solved by second-order finite difference method without handling coordinate singularities. The solver was further extended to study the dynamics of a diffusiophoretic particle suspended in Stokes flow. Numerical experiments suggested that the particle can achieve a self-sustained unidirectional motion at moderate Peclet numbers, whereas the particle motion becomes chaotic in high Peclet number regimes. The statistical analysis illustrates the run-and-tumble-like nature at short times and diffusive nature at long times without any source of noise.