Abstract
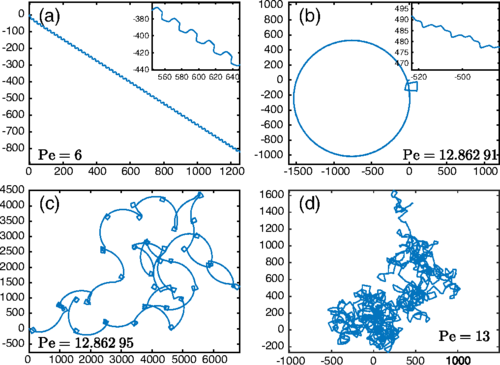
The swimming of a rigid phoretic particle in an isotropic fluid is studied numerically as a function of the dimensionless solute emission rate (or Péclet number Pe). The particle sets into motion at a critical Pe. Whereas the particle trajectory is straight at a small enough Pe, it is found that it loses its stability at a critical Pe in favor of a meandering motion. When Pe is increased further, the particle meanders at a short scale but its trajectory wraps into a circle at a larger scale. Increasing even further, Pe causes the swimmer to escape momentarily the circular trajectory in favor of chaotic motion, which lasts for a certain time, before regaining a circular trajectory, and so on. The chaotic bursts become more and more frequent as Pe increases, until the trajectory becomes fully chaotic, via the intermittency scenario. The statistics of the trajectory is found to be of the run-and-tumble-like nature at a short enough time and of diffusive nature at a long time without any source of noise.